
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.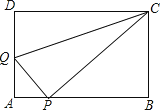
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.
【答案】
(1)
【解答】解:∵△CDQ≌△CPQ,
∴DQ=PQ,PC=DC,
∵AB=DC=5,AD=BC=3,
∴PC=5,
在Rt△PBC中,PB=![]() =4,
=4,
∴PA=AB﹣PB=5﹣4=1,
设AQ=x,则DQ=PQ=3﹣x,
在Rt△PAQ中,(3﹣x)2=x2+12,
解得x=![]() ,
,
∴AQ=![]() .
.
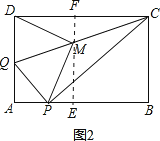
(2)
如图2,过M作EF⊥CD于F,则EF⊥AB,
∵MD⊥MP,
∴∠PMD=90°,
∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,
∴∠MDF=∠PME,
∵M是QC的中点,
根据直角三角形直线的性质求得DM=PM=![]() QC,
QC,
在△MDF和△PME中,
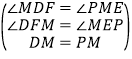 ,
,
∴△MDF≌△PME(AAS),
∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF=![]() DC=
DC=![]() ,
,
∴ME=![]() ,
,
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.
【解析】(1)根据全等三角形的性质求得DQ=PQ,PC=DC=5,然后利用勾股定理即可求得;
(2)过M作EF⊥CD于F,则EF⊥AB,先证得△MDF≌△PME,求得ME=DF=![]() ,然后根据梯形的中位线的性质定理即可求得.
,然后根据梯形的中位线的性质定理即可求得.
【考点精析】通过灵活运用勾股定理的概念和矩形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c的顶点为P,与y轴交于点A,与直线OP交于点B.
(1)如图1,若点P的横坐标为1,点B的坐标为(3,6),试确定抛物线的解析式;
(2)在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM=3,求点M的坐标;
(3)如图2,若点P在第一象限,且PA=PO,过点P作PD⊥x轴于点D.将抛物线y=x2+bx+c平移,平移后的抛物线经过点A、D,该抛物线与x轴的另一个交点为C,请探究四边形OABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.
(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;
(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则![]() 等于( )
等于( )
A.![]()
B.2
C.1.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9![]()
B.18![]()
C.36![]()
D.72![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数y=![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( ) 
A.![]() π
π
B.![]() +1
+1
C.π
D.π+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com