
【题目】在平面直角坐标系xOy中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标.
【答案】解:分两种情况;
①如图1,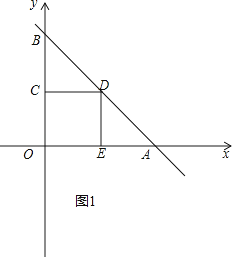
令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=![]() OA=
OA=![]() ,
,
∴E(![]() ,0);
,0);
②如图2,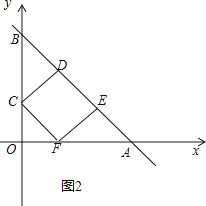
由①知△OFC,△EFA是等腰直角三角形,
∴CF=![]() OF,AF=
OF,AF=![]() EF,
EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=![]() OF=2OF,
OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
【解析】分两种情况:①如图1,令x=0,则y=3,令y=0,则x=3,得到OA=OB=3,∠BAO=45°,根据DE⊥OA,推出DE=AE,由于四边形COED是正方形,得到OE=DE,等量代换得到OE=AE,即可得到结论;②如图2,由(1)知△OFC,△EFA是等腰直角三角形,由四边形CDEF是正方形,得到EF=CF,于是得到AF=![]() OF=2OF,求出OA=OF+2OF=3,即可得到结论.
OF=2OF,求出OA=OF+2OF=3,即可得到结论.
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长。
,求BH的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=![]() BM.
BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.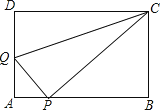
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.
(1)求证:BC是⊙O的切线;
(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC=![]() ,AD=3,求直径AB的长.
,AD=3,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF. 
(1)求证:FG=FB.
(2)若tan∠F= ![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com