
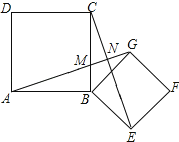
【题目】如图,四边形ABCD、为正方形,连接AG、CE.
(1)
求证:AG=CE;
(2)求证:AG⊥CE.
【答案】
(1)
证明:∵四边形ABCD、BEFG均为正方形,
∴AB=CB,∠ABC=∠GBE=90°,BG=BE,
∴∠ABG=∠CBE,
在△ABG和△CBE中,
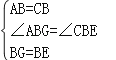 ,
,
∴△ABG≌△CBE(SAS),
∴AG=CE;
(2)
证明:如图所示:∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠ABC=90°,
∴∠BAG+∠AMB=90°,
∵∠AMB=∠CMN,
∴∠BCE+∠CMN=90°,
∴∠CNM=90°,
∴AG⊥CE.
【解析】(1)由正方形的性质得出AB=CB,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,由SAS证明△ABG≌△CBE,得出对应边相等即可;
(2)由△ABG≌△CBE,得出对应角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
此题根据全等三角形的判定和正方形的相关性质即可解答。


科目:初中数学 来源: 题型:
【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( ) 
A.前2分钟,乙的平均速度比甲快
B.甲、乙两人8分钟各跑了800米
C.5分钟时两人都跑了500米
D.甲跑完800米的平均速度为100米/分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市开展“五城联创”活动中,某工程队承担了某小区900米长的污水管道改造任务.工程队在改造完360米管道后,引进了新设备,每天的工作效率比原来提高了20%,结果共用27天完成了任务,问引进新设备前工程队每天改造管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为 元.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.
(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;
(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A、B的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D、E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.
(1)求证:GC是⊙O的切线;
(2)求DE的长;
(3)过点C作CF⊥DE于点F,若∠CED=30°,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
A.9![]()
B.18![]()
C.36![]()
D.72![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图, 
请你根据统计图解答下列问题:
(1)李老师一共调查了多少名同学?
(2)C类女生有名,D类男生有名,将下面条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com