Question

【题目】如图，AB是⊙O的直径，AB=6，过点O作OH⊥AB交圆于点H，点C是弧AH上异于A、B的动点，过点C作CD⊥OA，CE⊥OH，垂足分别为D、E，过点C的直线交OA的延长线于点G，且∠GCD=∠CED．

（1）求证：GC是⊙O的切线；
（2）求DE的长；
（3）过点C作CF⊥DE于点F，若∠CED=30°，求CF的长．

Answer 1

【答案】
（1）

证明：连接OC，交DE于M，如图所示：

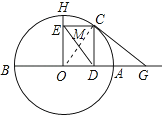
∵OH⊥AB，CD⊥OA，CE⊥OH，∴∠DOE=∠OEC=∠ODC=90°，∴四边形ODCE是矩形，∴∠DCE=90°，DE=OC，MC=MD，

∴∠CED+∠MDC=90°，∠MDC=∠MCD，∵∠GCD=∠CED，∴∠GCD+∠MCD=90°，即GC⊥OC，∴ GC是⊙O的切线

（2）

解：由（1）得：DE=OC=AB=3；

（3）

解：∵∠DCE=90°，∠CED=30°，∴CE=DEcos∠CED=3×=，∴ CF=CE=

【解析】（1）先证明四边形ODCE是矩形，得出∠DCE=90°，DE=OC，MC=MD，得出∠CED+∠MDC=90°，∠MDC=∠MCD，证出∠GCD+∠MCD=90°，即可得出结论；（2）由（1）得：DE=OC=AB，即可得出结果；（3）运用三角函数求出CE，再由含30°角的直角三角形的性质即可得出结果．