Question

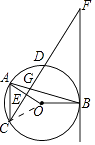
【题目】如图，点A、B、C、D均在⊙O上，FB与⊙O相切于点B，AB与CF交于点G，OA⊥CF于点E，AC∥BF．
（1）求证：FG=FB．
（2）若tan∠F= ，⊙O的半径为4，求CD的长．

Answer 1

【答案】
（1）证明：∵OA=OB，

∴∠OAB=∠OBA，

∵OA⊥CD，

∴∠OAB+∠AGC=90°．

∵FB与⊙O相切，

∴∠FBO=90°，

∴∠FBG+OBA=90°，

∴AGC=∠FBG，

∵∠AGC=∠FGB，

∴∠FGB=∠FBG，

∴FG=FB

（2）解：如图，

设CD=a，

∵OA⊥CD，

∴CE= CD= a．

∵AC∥BF，

∴∠ACF=∠F，

∵tan∠F=

tan∠ACF= = ，即 = ，

解得AE= a，

连接OC，OE=4﹣ a，

∵CE2+OE2=OC2，

∴（ a）2+（4﹣ a）2=4，

解得a= ，

CD=

【解析】（1）根据等腰三角形的性质，可得∠OAB=∠OBA，根据切线的性质，可得∠FBG+OBA=90°，根据等式的性质，可得∠FGB=∠FBG，根据等腰三角形的判定，可得答案；（2）根据平行线的性质，可得∠ACF=∠F，根据等角的正切值相等，可得AE，根据勾股定理，可得答案．