
分析 (1)利用待定系数法即可求得;
(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标和对称轴方程即可;
(3)根据图象即可得出,当-3≤x≤1时,y≤0.
解答 解:(1)函数y=x2+bx-3的图象经过点(1、0),
∴1+b-3=0,解得b=2;
∴函数解析式为y=x2+2x-3.
(2)∵y=x2+2x-3=(x+1)2-4,
∴顶点坐标:(-1,-4),
对称轴为直线x=-1;
(3)如图,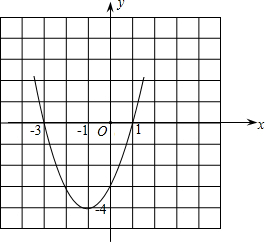
当-3≤x≤1时,y≤0.
点评 主要考查了待定系数法求二次函数的解析式和函数图象的性质,主要利用了顶点式解析式求出顶点坐标和对称轴,会根据图象所在的位置关系求相关的变量的取值范围,熟记性质是解题的关键,作出图形更形象直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
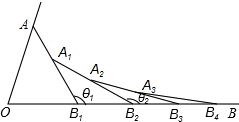 如图,已知∠AOB=α,在射线OA、OB上分别取点OA=OB1,连结AB1,在B1A、B1B上分别取点A1、B2,使B1B2=B1A1,连结A1B1…按此规律上去,记∠A1B1B2=θ1,∠A2B2B3=θ2,…,∠AnBnBn+1=θn,则:
如图,已知∠AOB=α,在射线OA、OB上分别取点OA=OB1,连结AB1,在B1A、B1B上分别取点A1、B2,使B1B2=B1A1,连结A1B1…按此规律上去,记∠A1B1B2=θ1,∠A2B2B3=θ2,…,∠AnBnBn+1=θn,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
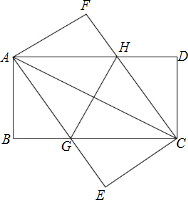 如图所示,已知在矩形ABCD和矩形AECF中,CD=CE,AD与CF相交于点H,BC与AE相交于点G,连接AC、GH.
如图所示,已知在矩形ABCD和矩形AECF中,CD=CE,AD与CF相交于点H,BC与AE相交于点G,连接AC、GH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
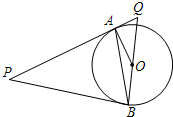 如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F.G,则弧FG对的圆周角∠FPG的大小为( )
如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F.G,则弧FG对的圆周角∠FPG的大小为( )| A. | 45° | B. | 60° | C. | 75° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com