
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.

(1)求证:DF为⊙O的切线;
(2)若AB=4,∠C=30°,求劣弧![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
【解析】(1)连接AD、OD,根据直径所对的圆周角为直角,可得∠ADB=90°,然后根据等腰三角形的性质求出BD=CD,再根据中位线的性质求出OD⊥DF,进而根据切线的判定证明即可;
(2)连接OE,根据三角形的外角求出∠BAE的度数,然后根据圆周角定理求出∠BOE的度数,根据弧长公式求解即可.
(1)连接AD、OD.∵AB是直径,∴∠ADB=90°.
∵AB=AC,∴BD=CD,
又∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∵DF⊥AC,∴OD⊥DF
即∠ODF=90°.∴DF为⊙O的切线;
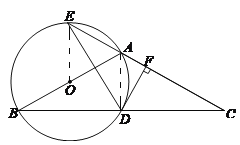
(2)连接OE.∵AB=AC,∴∠B=∠C=30°,∴∠BAE=60°,
∵∠BOE=2∠BAE,∴∠BOE=120°,
∴![]() =
=![]() ·4π=
·4π=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.

(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且始终保持
边上运动,且始终保持![]() .连接
.连接![]() 、
、![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)试证明![]() 是等腰直角三角形;
是等腰直角三角形;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:已知∠MAB=60°,以AB的长为菱形ABCD的边长,点D在AM上,
(1)作出这个菱形.(保留作图痕迹,不写作法,不用证明)
(2)若AB=2,则对角线AC的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的学习生活,某班组织学生参观某爱国主义教育基地,所联系的旅行社收费标准如下:
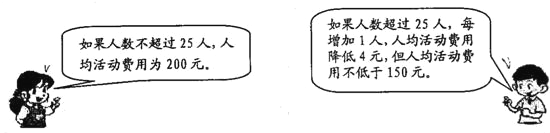
活动结束后,该班共支付给该旅行社活动费用5600元,该班共有多少人参加这次活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).
(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;
(2)当t为多少时,△PQB是以PQ为腰的等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种树苗,栽种时高度约为80厘米,为研究它的生长情况,测得数据如下表:
(1)此变化过程中_____是自变量,_____是因变量;
(2)树苗高度h与栽种的年数n的关系式为_____;
(3)栽种后_____后,树苗能长到280厘米.
栽种以后的年数n/年 | 高度h/厘米 |
1 | 105 |
2 | 130 |
3 | 155 |
4 | 180 |
… | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com