
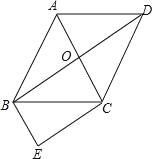
【题目】(2016云南省第18题)如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
【答案】(1)、![]() ;(2)、证明过程见解析.
;(2)、证明过程见解析.
【解析】
试题分析:(1)、由四边形ABCD是菱形,得到对边平行,且BD为角平分线,利用两直线平行得到一对同旁内角互补,根据已知角之比求出相应度数,进而求出∠BDC度数,即可求出tan∠DBC的值;(2)、由四边形ABCD是菱形,得到对角线互相垂直,利用两组对边平行的四边形是平行四边形,再利用有一个角为直角的平行四边形是矩形即可得证.
试题解析:(1)、∵四边形ABCD是菱形, ∴AD∥BC,∠DBC=![]() ∠ABC, ∴∠ABC+∠BAD=180°,
∠ABC, ∴∠ABC+∠BAD=180°,
∵∠ABC:∠BAD=1:2, ∴∠ABC=60°, ∴∠BDC=![]() ∠ABC=30°, 则tan∠DBC=tan30°=
∠ABC=30°, 则tan∠DBC=tan30°=![]() ;
;
(2)、∵四边形ABCD是菱形, ∴AC⊥BD,即∠BOC=90°, ∵BE∥AC,CE∥BD, ∴BE∥OC,CE∥OB,
∴四边形OBEC是平行四边形, 则四边形OBEC是矩形.


科目:初中数学 来源: 题型:
【题目】(2016山西省第22题)(本题12分)综合与实践
问题情境
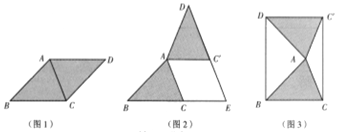
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(![]() )沿对角线AC剪开,得到
)沿对角线AC剪开,得到![]() 和
和![]() .
.
操作发现
(1)将图1中的![]() 以A为旋转中心,逆时针方向旋转角
以A为旋转中心,逆时针方向旋转角![]() ,使
,使 ![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长BC 和
,分别延长BC 和![]() 交于点E,则四边形
交于点E,则四边形![]() 的状是 ;
的状是 ;
(2)创新小组将图1中的![]() 以A为旋转中心,按逆时针方向旋转角
以A为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所
,得到如图3所
示的![]() ,连接DB,
,连接DB,![]() ,得到四边形
,得到四边形![]() ,发现它是矩形.请你证明这个论;
,发现它是矩形.请你证明这个论;
(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将![]() 沿着射线DB方向平移acm,得到
沿着射线DB方向平移acm,得到![]() ,连接
,连接![]() ,
,![]() ,使四边形
,使四边形![]() 恰好为正方形,求a的值.请你解答此问题;
恰好为正方形,求a的值.请你解答此问题;
(4)请你参照以上操作,将图1中的![]() 在同一平面内进行一次平移,得到
在同一平面内进行一次平移,得到![]() ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
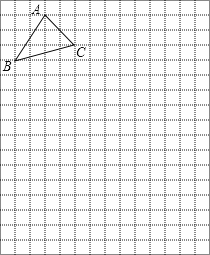
【题目】在如图所示的网格中,三角形ABC的顶点A(0,5),B(-2,2).
(1)根据A,B坐标在网格中建立平面直角坐标系,并写出点C坐标:( );
(2)平移三角形ABC,使点C移动到点F(7,-4),画出平移后的三角形DEF,其中点D与点A对应,点E与点B对应.
查看答案和解析>>
科目:初中数学 来源: 题型:
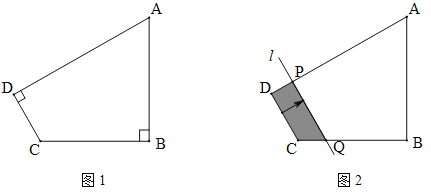
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣4的图象先向右平移2个单位,再向上平移3个单位后得到的抛物线的函数表达式为( )
A.y=(x+2)2﹣7
B.y=(x﹣2)2﹣7
C.y=(x+2)2﹣1
D.y=(x﹣2)2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com