
【题目】(2016山西省第22题)(本题12分)综合与实践
问题情境
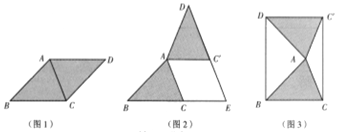
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(![]() )沿对角线AC剪开,得到
)沿对角线AC剪开,得到![]() 和
和![]() .
.
操作发现
(1)将图1中的![]() 以A为旋转中心,逆时针方向旋转角
以A为旋转中心,逆时针方向旋转角![]() ,使
,使 ![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长BC 和
,分别延长BC 和![]() 交于点E,则四边形
交于点E,则四边形![]() 的状是 ;
的状是 ;
(2)创新小组将图1中的![]() 以A为旋转中心,按逆时针方向旋转角
以A为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所
,得到如图3所
示的![]() ,连接DB,
,连接DB,![]() ,得到四边形
,得到四边形![]() ,发现它是矩形.请你证明这个论;
,发现它是矩形.请你证明这个论;
(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将![]() 沿着射线DB方向平移acm,得到
沿着射线DB方向平移acm,得到![]() ,连接
,连接![]() ,
,![]() ,使四边形
,使四边形![]() 恰好为正方形,求a的值.请你解答此问题;
恰好为正方形,求a的值.请你解答此问题;
(4)请你参照以上操作,将图1中的![]() 在同一平面内进行一次平移,得到
在同一平面内进行一次平移,得到![]() ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
【答案】(1)、菱形;(2)、证明过程见解析;(3)、![]() 或
或![]() ;(4)、平行四边形.
;(4)、平行四边形.
【解析】
试题分析:(1)、利用旋转的性质和菱形的判定证明;(2)、利用旋转的性质以及矩形的判定证;(3)、利用平移行性质和正方形的判定证明,需注意射线这个条件,所以需要分两种情况当点![]() 在边
在边![]() 上和点
上和点![]() 在边
在边![]() 的延长线上时;(4)、开放型题目,答对即可.
的延长线上时;(4)、开放型题目,答对即可.
试题解析:(1)、菱形
(2)、作![]() 于点E. 由旋转得
于点E. 由旋转得![]() ,
,![]() .
.
![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
同理![]() ,
,![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,![]() ,
,![]() , ∴四边形
, ∴四边形![]() 是矩形
是矩形
(3)、过点B作![]() ,垂足为F,
,垂足为F,![]() ,
, ![]() .
.
在Rt![]() 中,
中,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
, ![]() .
.
![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,![]() .
.
当四边形![]() 恰好为正方形时,分两种情况:
恰好为正方形时,分两种情况:
①点![]() 在边
在边![]() 上.
上.![]() .
.
②点![]() 在边
在边![]() 的延长线上,
的延长线上,![]()
综上所述,a的值为![]() 或
或![]() .
.
(4)、答案不唯一.
平移及构图方法:将![]() 沿着射线CA方向平移,平移距离为
沿着射线CA方向平移,平移距离为![]() 的长度,得到
的长度,得到![]() ,连接
,连接![]() .
.
结论:四边形是平行四边形



 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
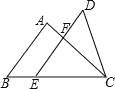
【题目】(2016浙江省舟山市第15题)如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x﹣4=0,下列变形正确的是( )
A.(x﹣6)2=﹣4+36
B.(x﹣6)2=4+36
C.(x﹣3)2=﹣4+9
D.(x﹣3)2=4+9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用全面调查的是( )
A. 了解泰安市所有中学生的视力情况
B. 了解某校七(4)班学生校服的尺码情况
C. 调查北京2017年的游客流量
D. 调查中国“2018俄罗斯世界杯”栏目的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+1)2+b=0的解是( )
A. x1=﹣3,x2=0 B. x1=0,x2=3
C. x1=﹣4,x2=﹣1 D. x1=1,x2=4
查看答案和解析>>
科目:初中数学 来源: 题型:
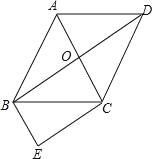
【题目】(2016云南省第18题)如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com