
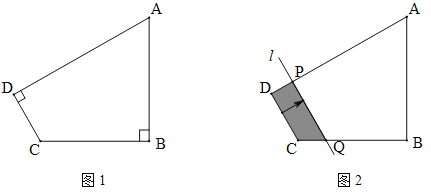
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() ).
).
【解析】
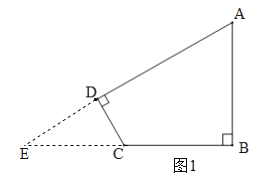
试题分析:(1)分别延长AD、BC相交于点E,在Rt△ABE中,解直角三角形可得BE,EC,AE的长,又∠E+∠A=90°,∠E+∠ECD=90°,得到∠A=∠ECD,由tanA=![]() ,得到cosA= cos∠ECD =
,得到cosA= cos∠ECD =![]() ,从而得到CD的长;
,从而得到CD的长;
(2)由(1)可知tan∠ECD=![]() ,得到ED=
,得到ED=![]() ,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=
,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=![]() ,由
,由![]() ,得到y=
,得到y=![]() ,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=
,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=![]() ,故可得自变量x的取值范围.
,故可得自变量x的取值范围.
试题解析:(1)如图1,分别延长AD、BC相交于点E,在Rt△ABE中,∵tanA=![]() ,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=
,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=![]() ,∴cosA=
,∴cosA=![]() ,∴cos∠ECD=
,∴cos∠ECD=![]() ,∴CD=
,∴CD=![]() ;
;
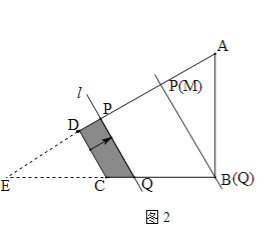
(2)由(1)可知tan∠ECD=![]() ,∴ED=
,∴ED=![]() ,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴
,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴![]() ,∴
,∴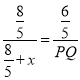 ,即PQ=
,即PQ=![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() =
=![]() ,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=
,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=![]() ,∴自变量x的取值范围为:
,∴自变量x的取值范围为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用全面调查的是( )
A. 了解泰安市所有中学生的视力情况
B. 了解某校七(4)班学生校服的尺码情况
C. 调查北京2017年的游客流量
D. 调查中国“2018俄罗斯世界杯”栏目的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+1)2+b=0的解是( )
A. x1=﹣3,x2=0 B. x1=0,x2=3
C. x1=﹣4,x2=﹣1 D. x1=1,x2=4
查看答案和解析>>
科目:初中数学 来源: 题型:
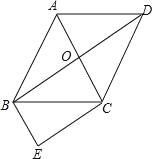
【题目】(2016云南省第18题)如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
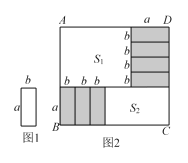
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S2-S1的值为 .
(2)当AD=40时,请用含a、b的式子表示 S2-S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2-S1 的值总保持不变,则a、b 满足的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
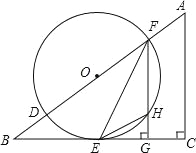
【题目】(2016广东省茂名市第24题)如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com