
证明题(本题8分,每空1分)
已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
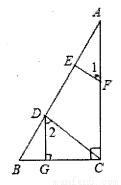
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG//AC(___________________________________),
∴∠2=_______(___________________________________),
∵∠1=∠2(______________),
∴∠1=∠DCA(等量代换),
∴EF//CD(___________________________________),
∴∠AEF=∠ADC(__________________________________),
∵EF⊥AB(已知)
∴∠AEF=90°(___________________________________),
∴∠ADC=90°
∴CD⊥AB(___________________________________).
同旁内角互补两直线平行;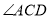 ;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
【解析】
试题分析:首先证得DG//AC,再应用平行线的判定证得EF//CD,进一步证得∠ADC=90°,即CD⊥AB.
试题解析:证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义),
∴DG//AC(同旁内角互补两直线平行),
∴∠2=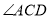 (两直线平行,内错角相等),
(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF//CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知)
∴∠AEF=90°(垂直的定义),
∴∠ADC=90°
∴CD⊥AB(垂直的定义).
故答案为:同旁内角互补两直线平行;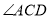 ;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
;两直线平行,内错角相等;已知;同位角相等,两直线平行;两直线平行,同位角相等;垂直的定义;垂直的定义.
考点:平行线的判定和性质;垂直的定义.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF= ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市八年级下学期第一次月考数学试卷(解析版) 题型:选择题
在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A、42 B、32 C、42或32 D、37或33
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市八年级下学期第一次月考数学试卷(解析版) 题型:选择题
等式4(x-2)>2(3x+5)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台第一教研片七年级下学期第一次月考数学卷(解析版) 题型:选择题
如下图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO= a°,则下列结论: ①∠BOE=
a°,则下列结论: ①∠BOE=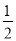 (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台第一教研片七年级下学期第一次月考数学卷(解析版) 题型:选择题
下列计算正确的是( ).
A.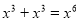 B.
B.
C. D.(2xy)3=2x3y
D.(2xy)3=2x3y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com