
分析 首先解每个不等式,三个不等式的解集的公共部分就是所求不等式组的解集,然后确定最小的整数解即可.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}≥\frac{x-1}{3}…①}\\{3x-2>x+2…②}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x…③}\end{array}\right.$,
解①得:x≥-2,
解②得:x>2,
解③得:x≤4.
则不等式组的解集是:2<x≤4.
最小的整数解是:3.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.


科目:初中数学 来源: 题型:解答题
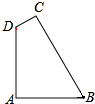 如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°.设P=BC+CD,四边形ABCD的面积为S.
如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°.设P=BC+CD,四边形ABCD的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=3}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=1}\\{b=7}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com