
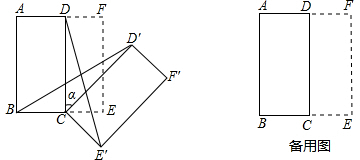
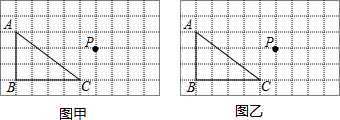
分析 (1)根据旋转的性质得∠D′CB=∠DCE′,然后根据“SAS”可判断△BCD′≌△E′CD,则BD′=E′D;
(2)若α=135°,则∠DCD′=135°=∠HCD′,符合SAS的判定定理.
解答 解:(1)∵∠D′CB=90°+α,∠DCE′═90°+α,
∴∠D′CB=∠DCE′,
在△BCD′和△E′CD中,
$\left\{\begin{array}{l}{BC=CE′=1}\\{∠D′CB=∠DCE′}\\{CD′=CD}\end{array}\right.$
∴△BCD′≌△E′CD(SAS),
∴BD′=E′D;
(2)能. α=135°或α=315°;
若α=135°,则∠DCD′=135°=∠HCD′,
在△DCD′与△HCD′中,
$\left\{\begin{array}{l}{DC=HC=2}\\{∠DCD′=135°=∠HCD′}\\{CD′=CD′}\end{array}\right.$,
∴△DCD′≌△HCD′.
点评 本题考查了旋转的性质,以及三角形全等的判定和性质,熟练掌握性质定理是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:选择题
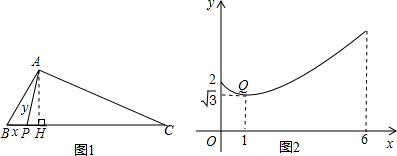
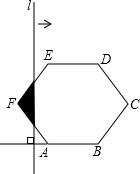 如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )
如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )| A. | 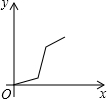 | B. | 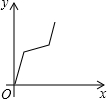 | C. | 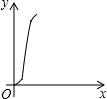 | D. | 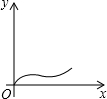 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
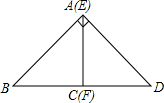 数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.
数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.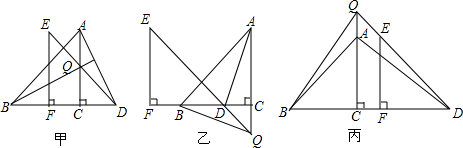
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

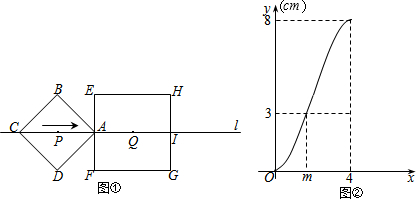
| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
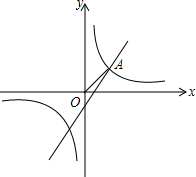 如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.
如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com