
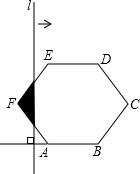
 如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )
如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )| A. | 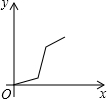 | B. | 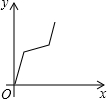 | C. | 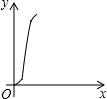 | D. | 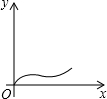 |
分析 根据直线l⊥AB、且从点F开始向右匀速平行移动,扫过正六边形ABCDEF的阴影部分的面积y的变换趋势及快慢,进而得到函数的图象.
解答 解:直线l⊥AB、且从点F开始向右匀速平行移动,扫过正六边形ABCDEF的面积(阴影部分)为y,移动的时间为x,
当l从经过F到经过E时,阴影部分的面积y随x的增大而增大,而且增加的速度越来越快,则其图象应该是凹增的;
当l从经过点E到经过D时,阴影部分的面积y随x的增大而增大,而且增加的速度不变;
当l从经过点D到经过C时,阴影部分的面积y随x的增大而增大,而且增加的速度越来越慢,则其图象应该是凸增的;
分析四个答案中的图象,只有C符合条件;
故选:C.
点评 本题考查的知识点是函数的图象,其中根据现实问题分析出图象的变化趋势,进而判断其图象的形状是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
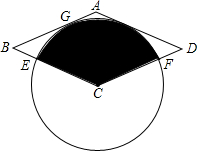 如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.
如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com