
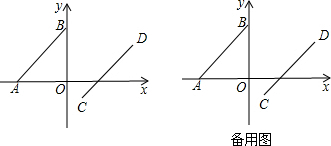
分析 (1)根据非负数的性质,得到a+3=0,a=b=0,即可解答;
(2)求出直线CD解析式,设点P的坐标为(0,m),求出点P到直线CD的距离,根据面积公式列出方程,即可解答;
(3)由平移可知AB∥CD,根据平行线的性质,角平分线的性质,三角形外角的性质可得∠AMC与∠ANC的数量关系.
解答 解:(1)∵$\sqrt{a+3}$+|a+b|=0,
∴a+3=0,a+b=0,
解得:a=-3,b=3,
∴A(-3,0),B(0,3).
(2)∵A(-3,0),B(0,3).
∴AB=$\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}$
∵线段AB向右平移4个单位,再向下平移1个单位,A点的对应点为C,B点的对应点为D,
∴C(1,-1),D(4,2),CD=3$\sqrt{2}$
设直线CD的解析式为y=kx+b,
把C(1,-1),D(4,2)代入得:$\left\{\begin{array}{l}{k+b=-1}\\{4k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴y=x-2,
设点P的坐标为(0,m),
则点P到直线CD的距离为;h=$\frac{|0-m-2|}{\sqrt{{1}^{2}+(-1)^{2}}}=\frac{|m+2|}{\sqrt{2}}$,
∵S△CDP=3,
∴$\frac{1}{2}×\frac{|2+m|}{\sqrt{2}}×3\sqrt{2}=3$,
∴|2+m|=2,
∴m=0或m=-4,
∴点P的坐标为(0,0)或(0,-4).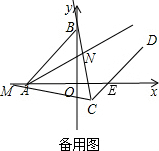 (3)如图,
(3)如图,
由平移可知AB∥CD,
∴∠ABN=∠BCE,∠BAE+∠AED=180°,
∵∠BAO与∠DCM的平分线交于N,
∴∠BAN=∠NAE,∠BCM=∠BCD,
∴2∠ANC=2∠ABN+2∠BAN=∠MCD+∠BAE,∠AMC=∠AED-∠MCD,
∴2∠ANC+∠AMC=∠MCD+∠BAE+∠AED-∠MCD=∠BAE+∠AED=180°.
故∠AMC与∠ANC的数量关系为:2∠ANC+∠AMC=180°.
点评 考查了坐标与图形性质,涉及的知识点有:非负数的性质,待定系数法求直线解析式,勾股定理,三角形面积,平移,平行线的性质,角平分线的性质,三角形外角的性质,综合性较强,有一定的难度.


科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为$\frac{25}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
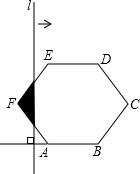 如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )
如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )| A. | 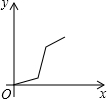 | B. | 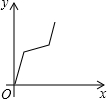 | C. | 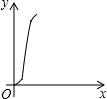 | D. | 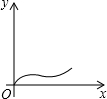 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
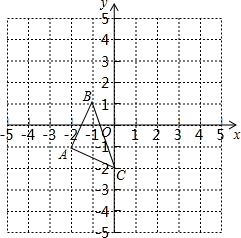 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
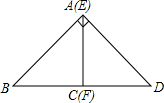 数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.
数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.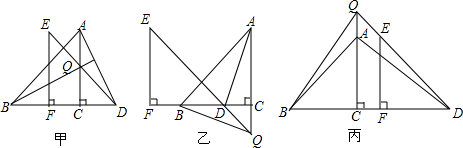
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

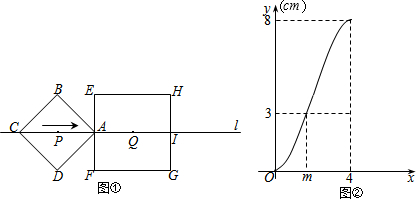
| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
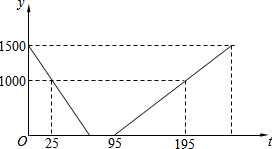 游泳池完成换水需要经过“排水-清洗-注水”三个过程.如图,图中折线表示的是游泳池在换水过程中池中的水量y(m3)与时间t(min)之间的关系.
游泳池完成换水需要经过“排水-清洗-注水”三个过程.如图,图中折线表示的是游泳池在换水过程中池中的水量y(m3)与时间t(min)之间的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com