
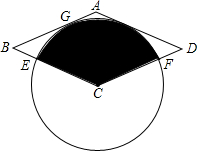
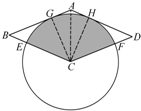
 如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.
如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.分析 (1)连接CG、AC,过点C作CH⊥AD,垂足为H,由AB与⊙C相切,根据切线的性质得到CG⊥AB,根据菱形的性质得到AC平分∠BAD,由角平分线的性质得到CG=CH,
于是结论可得;
(2)由已知条件∠A=135°,得到∠B=45°,在Rt△CBG中,求得CG=1,根据圆的面积公式即可得到结论.
解答 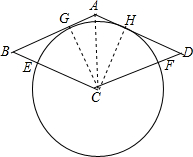
 (1)证明:连接CG、AC,过点C作CH⊥AD,垂足为H,
(1)证明:连接CG、AC,过点C作CH⊥AD,垂足为H,
∵AB与⊙C相切,
∴CG⊥AB,
∵四边形ABCD为菱形,
∴AC平分∠BAD,
∴CG=CH,
∴AD与⊙C相切;
(2)∵∠A=135°,
∴∠B=45°,
在Rt△CBG中,
∵∠B=45°,BC=AB=$\sqrt{2}$,
∴CG=1,
即:R=1,
设圆锥底面的半径为r,
则2πr=$\frac{nπR}{180}=\frac{135π}{180}$,
∴r=$\frac{3}{8}$,
∴圆锥底面圆的半径为$\frac{3}{8}$.
点评 本题考查了切线的性质和判定,菱形的性质,等腰直角三角形的性质,准确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
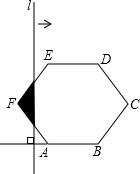 如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )
如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )| A. | 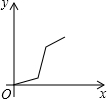 | B. | 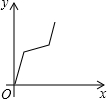 | C. | 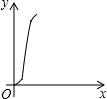 | D. | 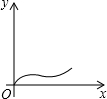 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
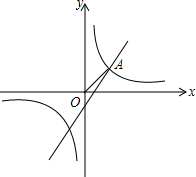 如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.
如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
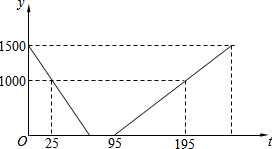 游泳池完成换水需要经过“排水-清洗-注水”三个过程.如图,图中折线表示的是游泳池在换水过程中池中的水量y(m3)与时间t(min)之间的关系.
游泳池完成换水需要经过“排水-清洗-注水”三个过程.如图,图中折线表示的是游泳池在换水过程中池中的水量y(m3)与时间t(min)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com