
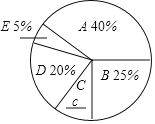
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
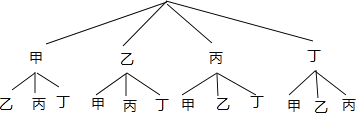
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
【答案】(1)32,8,10%;(2)96;(3)1200人;(4)![]() .
.
【解析】
(1)先根据“摘记法”的频数及其频率求得总人数,再根据频数、频率与总数间的关系可得a、b、c的值;
(2)总人数乘以样本中“反思法”学生所占比例可得;
(3)利用总人数乘以撰写读后感法的百分比即可解答
(4)用树状图表示出四人中随机抽取两人有12种可能,即可解答
解:(1)本次调查的学生有:20÷25%=80,
a=80×40%=32,
b=80×(100﹣40﹣25﹣20﹣5)%=80×10%=8,
c=(100﹣40﹣25﹣20﹣5)%=10%,
故答案为:32,8,10%;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有:960×10%=96人,
故答案为:96;
(3)同意小明的观点;理由如下:
全县6000名中学生中采用“撰写读后感法”读书的有:6000×20%=1200人;
(4)树状图如图所示,
∵从四人中随机抽取两人有12种可能,恰好是甲和乙的有2种可能,
∴抽取两人恰好是甲和乙的概率是![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
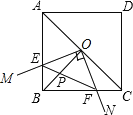
【题目】如图,已知在正方形ABCD中,点O是对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA;⑤AE2+BE2=2OPOB.其中正确的个数有( )个.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线一定过原点②方程ax2+bx+c=0(a≠0)的解为x=0或x=4,③a﹣b+c<0;④当0<x<4时,ax2﹣bx+c<0;⑤当x<2时,y随x增大而增大,其中结论正确的个数( )
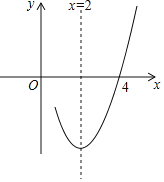
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
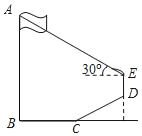
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
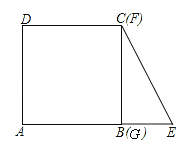
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
A.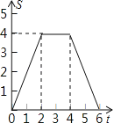 B.
B.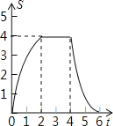
C.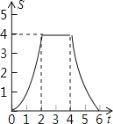 D.
D.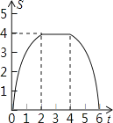
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
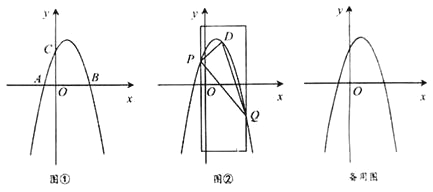
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
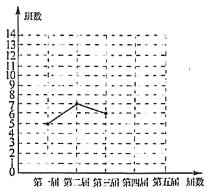
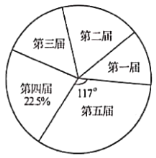
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com