
【题目】我们把对角线互相垂直的四边形叫做垂直四边形.
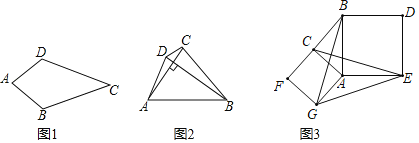
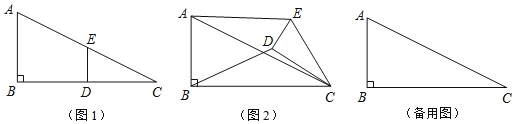
(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;
(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;
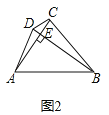
(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.
【答案】(1)四边形ABCD是垂直四边形;理由见解析;(2)见解析;(3)GE=![]()
【解析】
(1)由AB=AD,得出点A在线段BD的垂直平分线上,由CB=CD,得出点C在线段BD的垂直平分线上,则直线AC是线段BD的垂直平分线,即可得出结果;
(2)设AC、BD交于点E,由AC⊥BD,得出∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+DE2+CE2,即可得出结论;
(3)连接CG、BE,由正方形的性质得出AG=AC,AB=AE,![]() ,
,![]() ,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,推出∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,得出四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,
,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,推出∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,得出四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,![]() ,
,![]() ,代入计算即可得出结果.
,代入计算即可得出结果.
(1)解:四边形ABCD是垂直四边形;理由如下:
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂直四边形;
(2)证明:设AC、BD交于点E,如图2所示:
∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得:AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+DE2+CE2,
∴AD2+BC2=AB2+CD2;
(3)解:连接CG、BE,如图3所示:
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,![]() ,
,![]() ,∠CAG=∠BAE=90°,
,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,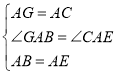 ,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
又∵∠AEC+∠CEB+∠ABE=90°,
∴∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,
∴四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,
∵AC=4,BC=3,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴GE=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书总的经费不超过1100元,要求购买的乙种图书是甲种图书的2倍,则甲种图书至多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(![]() ,0),与y轴的交点B在(0,0)和(0,﹣1)之间(不包括这两点),对称轴为直线x=
,0),与y轴的交点B在(0,0)和(0,﹣1)之间(不包括这两点),对称轴为直线x=![]() .则下列结论:① x>3时,y<0;② 4a+b<0;③﹣
.则下列结论:① x>3时,y<0;② 4a+b<0;③﹣![]() <a<0;④ 4ac+b2<4a.其中正确的是( )
<a<0;④ 4ac+b2<4a.其中正确的是( )
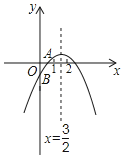
A.②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 和
和![]() 在第一象限内的图像如图,P是
在第一象限内的图像如图,P是![]() 的图象上一动点, PC⊥ x轴于点 C,交 的图象于点 A,PD ⊥y 轴于点D,交
的图象上一动点, PC⊥ x轴于点 C,交 的图象于点 A,PD ⊥y 轴于点D,交![]() 的图像于点B,当点P在
的图像于点B,当点P在![]() 的图像上运动时,下列结论错误的是( )
的图像上运动时,下列结论错误的是( )
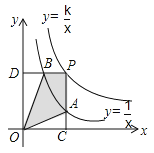
A.△ODB与△OCA的面积相等B.当点 A 是 PC 的中点时,点 B 一定是 PD 的中点
C.![]() D.当四边形 OCPD 为正方形时,四边形 PAOB 的面积最大
D.当四边形 OCPD 为正方形时,四边形 PAOB 的面积最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,线段
,线段![]() 、
、![]() 的长是一元二次方程
的长是一元二次方程![]() 的两根
的两根![]() ,
,![]() ,点
,点![]() 的横坐标为3,反比例函数
的横坐标为3,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
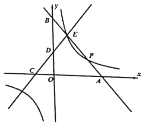
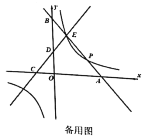
(1)若直线![]() 与反比例函数图象上除点
与反比例函数图象上除点![]() 外的另一交点为
外的另一交点为![]() ,求
,求![]() 的面积;若点
的面积;若点![]() 在
在![]() 轴上,若点
轴上,若点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值..
的最小值..
(2)若点![]() 在坐标轴上,在平面内是否存在一点
在坐标轴上,在平面内是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形且线段
为顶点的四边形是矩形且线段![]() 为矩形的一条边?若存在,直接写出符合条件的
为矩形的一条边?若存在,直接写出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的知识,拓展阅读视野,学习图书馆购买了一些科技、文学、历史等书籍,进行组合搭配成![]() 、
、![]() 、
、![]() 三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
三种套型书籍,发放给各班级的图书角供同学们阅读,已知各套型的规格与价格如下表:
|
|
| |
规格(本/套) | 12 | 9 | 7 |
价格(元/套) | 200 | 150 | 120 |
(1)已知搭配![]() 、
、![]() 两种套型书籍共15套,需购买书籍的花费是2120元,问
两种套型书籍共15套,需购买书籍的花费是2120元,问![]() 、
、![]() 两种套型各多少套?
两种套型各多少套?
(2)若图书馆用来搭配的书籍共有2100本,现将其搭配成![]() 、
、![]() 两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
两种套型书籍,这两种套型的总价为30750元,求搭配后剩余多少本书?
(3)若图书馆用来搭配的书籍共有122本,现将其搭配成![]() 、
、![]() 、
、![]() 三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
三种套型书籍共13套,且没有剩余,请求出所有搭配的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com