
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书总的经费不超过1100元,要求购买的乙种图书是甲种图书的2倍,则甲种图书至多能购买多少本?
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
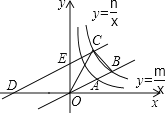
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() 和y=
和y=![]() 交于第一象限内的点A和B,且OA=2AB,将直线y=
交于第一象限内的点A和B,且OA=2AB,将直线y=![]() x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=
x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=![]() 交于点C,△OBC的面积为3.
交于点C,△OBC的面积为3.
(1)求m,n的值;
(2)点C到直线AB的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线W的图象与x轴交于A、O两点,顶点为点B(﹣1,﹣1).
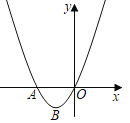
(1)求抛物线W的表达式;
(2)将抛物线W绕点A旋转180°得到抛物线V,使抛物线V的顶点为E,试通过计算判断抛物线V是否过点B;
(3)在抛物线W或V的图象上是否存在点D,使S△EBD=S△EBO?若存在,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.

(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
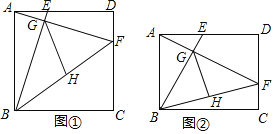
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
(1)求证:![]() ;
;
(2)线段![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙0的直径,点C在⊙0上,D是![]() 中点,若∠BAC=70°,求∠C.
中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整:
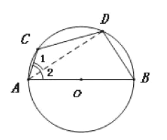
解:在⊙0中,
∵D是![]() 的中点
的中点
∴BD=CD.
∴∠1=∠2( )(填推理的依据).
∵∠BAC=70°,
∴∠2=35°.
∵AB是⊙0的直径,
∴∠ADB=90°( )(填推理的依据).
∴∠B=90°-∠2=55°.
∵A、B、C、D四个点都在⊙0上,
∴∠C+∠B=180°( )(填推理的依据).
∴∠C=180°-∠B= (填计算结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
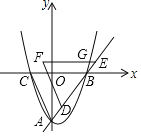
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,抛物线
与x轴交于点B,与y轴交于点A,抛物线![]() 经过A,B两点,与x轴的另一交点为C.
经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)将△ABC以每秒1个单位的速度沿射线AB方向平移,平移后的三角形记为△DEF,平移时间为t秒,0≤t≤5,平移过程中EF与抛物线交于点G.
①当FG:GE=3:2时,求t的值;
②△DEF与△AOB重叠部分面积为S,直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把对角线互相垂直的四边形叫做垂直四边形.
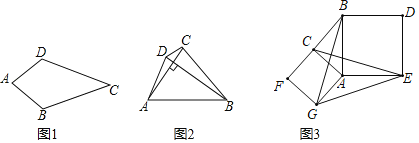
(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;
(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;
(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com