
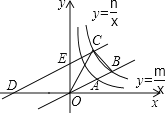
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() 和y=
和y=![]() 交于第一象限内的点A和B,且OA=2AB,将直线y=
交于第一象限内的点A和B,且OA=2AB,将直线y=![]() x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=
x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=![]() 交于点C,△OBC的面积为3.
交于点C,△OBC的面积为3.
(1)求m,n的值;
(2)点C到直线AB的距离是 .
【答案】(1)m=2,n=![]() ;(2)
;(2)![]()
【解析】
(1)根据直线解析式平移的规律得出y=![]() x向左平移4个单位后的解析式为y=
x向左平移4个单位后的解析式为y=![]() x+2,那么交y轴于E(0,2).作EF⊥OB于F,根据互相垂直的两直线斜率之积为-1且过点E,得到直线EF的解析式为y=-2x+2,与y=
x+2,那么交y轴于E(0,2).作EF⊥OB于F,根据互相垂直的两直线斜率之积为-1且过点E,得到直线EF的解析式为y=-2x+2,与y=![]() x联立,求出F(
x联立,求出F(![]() ,
,![]() ),根据两点间的距离公式得出EF=
),根据两点间的距离公式得出EF=![]() ,根据S△OBC=3,求出OB=
,根据S△OBC=3,求出OB=![]() ,由OA=2AB=
,由OA=2AB=![]() OB=
OB=![]() ,得出A(2,1),B(3,
,得出A(2,1),B(3,![]() ),将点A和B的坐标分别代入y=
),将点A和B的坐标分别代入y=![]() 和y=
和y=![]() ,即可求出m,n的值;
,即可求出m,n的值;
(2)点C到直线AB的距离等于EF的长.
(1)直线y=![]() x向左平移4个单位后的解析式为y=
x向左平移4个单位后的解析式为y=![]() (x+4),即y=
(x+4),即y=![]() x+2,
x+2,
∴直线y=![]() x+2交y轴于E(0,2),
x+2交y轴于E(0,2),
如图,作EF⊥OB于F,
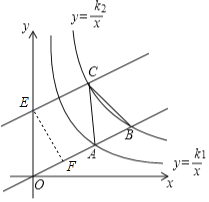
可得直线EF的解析式为y=﹣2x+2,
由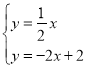 ,解得
,解得![]() ,
,
∴F(![]() ,
,![]() ),
),
∴EF=![]() =
=![]() ,
,
∵S△OBC=3,
∴![]() OBEF=3,
OBEF=3,
∴OB=![]() ,
,
∵OA=2AB=![]() OB=
OB=![]() ,
,
∴A(2,1),B(3,![]() ),
),
∴m=2,n=![]() ;
;
(2)∵CE∥OB,EF⊥OB于F,
∴点C到直线AB的距离=EF=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
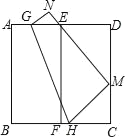
【题目】如图,将边长为3的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N,那么折痕GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
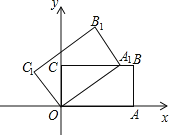
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
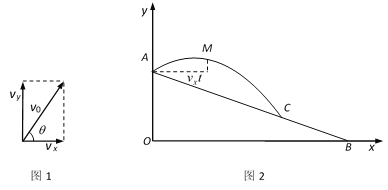
【题目】如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且![]() .图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为
.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为![]() ;M与A的水平距离为
;M与A的水平距离为![]() 米.已知该水流的初始速度
米.已知该水流的初始速度![]() 为15米/秒,水龙头的仰角θ为
为15米/秒,水龙头的仰角θ为![]() .
.
(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
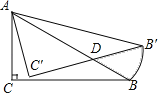
【题目】已知Rt△ABC中,∠C=90°,∠ABC=30°,AC=1.将Rt△ABC绕点A逆时针旋转15°后,得到Rt△AB'C',其中点B运动的路径为弧BB',那么图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
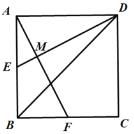
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
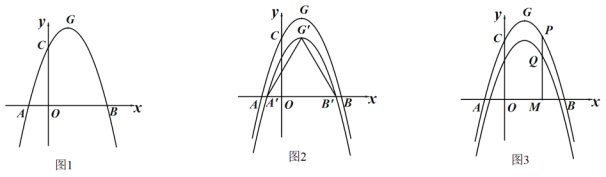
【题目】如图1,抛物线![]() :
:![]() 与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线
与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线![]() 的顶点为G.
的顶点为G.
(1)求出抛物线![]() 的解析式,并写出点G的坐标;
的解析式,并写出点G的坐标;
(2)如图2,将抛物线![]() 向下平移k(k>0)个单位,得到抛物线
向下平移k(k>0)个单位,得到抛物线![]() ,设
,设![]() 与x轴的交点为
与x轴的交点为![]() 、
、![]() ,顶点为
,顶点为![]() ,当△
,当△![]() 是等边三角形时,求k的值:
是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点(介于O与B之间),过点M作x轴的垂线分别交抛物线![]() 、
、![]() 于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了实现伟大的强国复兴梦,全社会都在开展“扫黑除恶”专项斗争,某区为了解各学校老师对“扫黑除恶”应知应会知识的掌握情况,对甲、乙两个学校各180名老师进行了测试,从中各随机抽取30名教师的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析,给出了部分成绩信息.
成绩(分) 频数 学校 | 90≤x<92 | 92≤x<94 | 94≤x<96 | 96≤x<98 | 98≤x≤100 |
甲校 | 2 | 3 | 5 | 10 | 10 |
甲校参与测试的老师成绩在96≤x<98这一组的数据是:96,96.5,97,97.5,97,96.5,97.5,96,96.5,96.5
甲、乙两校参与测试的老师成绩的平均数平均数、中位数、众数如下表:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 96.35 | m分 | 99分 |
乙校 | 95.85 | 97.5份 | 99分 |
根据以上信息,回答下列问题:
(1)m= ;
(2)在此次随机抽样测试中,甲校的王老师和乙校的李老师成绩均为97分,则在各自学校参与测试老师中成绩的名次相比较更靠前的是 (填“王”或“李”)老师,请写出理由;
(3)在此次随机测试中,乙校96分以上(含96分)的总人数比甲校96分以上(含96分)的总人数的2倍少100人,试估计乙校96分以上(含96分)的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com