
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,抛物线
与x轴交于点B,与y轴交于点A,抛物线![]() 经过A,B两点,与x轴的另一交点为C.
经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)将△ABC以每秒1个单位的速度沿射线AB方向平移,平移后的三角形记为△DEF,平移时间为t秒,0≤t≤5,平移过程中EF与抛物线交于点G.
①当FG:GE=3:2时,求t的值;
②△DEF与△AOB重叠部分面积为S,直接写出S与t的函数关系式.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)①t=
x﹣4;(2)①t=![]() ;②S=
;②S=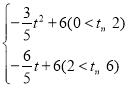
【解析】
(1)点A、B的坐标分别为:(0,﹣4)、(3,0),c=﹣4,抛物线的表达式为:y=![]() x2+bx﹣4,将点B的坐标代入上即可求解;
x2+bx﹣4,将点B的坐标代入上即可求解;
(2)①设点E(x,![]() t),FG:GE=3:2,则3EG=2FG,即3(3+
t),FG:GE=3:2,则3EG=2FG,即3(3+![]() ﹣x)=2(x+2﹣
﹣x)=2(x+2﹣![]() ),即可求解;
),即可求解;
②当0<t≤2时,S=S△BRF﹣S△OHR;②当2<t≤5时,S=![]() OB×|yD|,即可求解.
OB×|yD|,即可求解.
解:(1)直线![]() 与x轴交于点B,与y轴交于点A,
与x轴交于点B,与y轴交于点A,
令y=0,则x=3,令x=0,则y=﹣4,
故点A、B的坐标分别为:(0,﹣4)、(3,0),
c=﹣4,抛物线的表达式为:y=![]() x2+bx﹣4,
x2+bx﹣4,
将点B的坐标代入上式并解得:b=﹣![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)设△ABC沿AB移动了t个单位,则向右移动了![]() t个单位、向上移动了
t个单位、向上移动了![]() t个单位,
t个单位,
则点E、F、D的坐标分别为:(3+![]() t,
t,![]() t),(﹣2+
t),(﹣2+![]() t,
t,![]() t)、(
t)、(![]() t,﹣4+
t,﹣4+![]() t);
t);
①设点E(x,![]() t),
t),
FG:GE=3:2,则3EG=2FG,
即3(3+![]() ﹣x)=2(x+2﹣
﹣x)=2(x+2﹣![]() ),
),
化简得:x=1+![]() ,
,
将点E(1+![]() ,
,![]() )的坐标代入抛物线表达式并整理得:
)的坐标代入抛物线表达式并整理得:
3t2+3t﹣50=0,
解得:t=![]() (不合题意的值已舍去);
(不合题意的值已舍去);
②当0<t≤2时,
如下图所示,设直线FD与x、y轴分别交于点R、H,
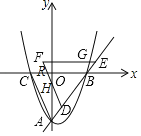
由点A、C的坐标可得,直线AC的表达式为:y=﹣2x﹣4,
则设直线FD的表达式为:y=﹣2x+b,
将点D的坐标代入上式并解得:b=2t﹣4,
故直线FD的表达式为:y=﹣2x+2t﹣4,
则点R、H的坐标分别为:(t﹣2,0)、(2t﹣4);
S=S△BRF﹣S△OHR
=![]() BR×|yD|﹣
BR×|yD|﹣![]() ×OR×OH
×OR×OH
=![]() (3﹣t+2)(﹣
(3﹣t+2)(﹣![]() t+4)﹣
t+4)﹣![]() (2﹣t)(4﹣2t)
(2﹣t)(4﹣2t)
=﹣![]() t2+6;
t2+6;
②当2<t≤5时,
S=![]() OB×|yD|=
OB×|yD|=![]() ×3×(4﹣
×3×(4﹣![]() t)=﹣
t)=﹣![]() t+6;
t+6;
综上,S=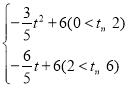 .
.


科目:初中数学 来源: 题型:
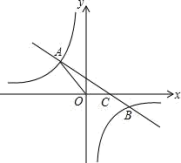
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书总的经费不超过1100元,要求购买的乙种图书是甲种图书的2倍,则甲种图书至多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2-(2a+2)x+b(a≠0)在x=0和x=6时函数值相等.
(1)求a的值;
(2)若该二次函数的图象与直线y=-2x的一个交点为(2,m),求它的解析式;
(3)在(2)的条件下,直线y=-2x-4与x轴,y轴分别交于A,B,将线段AB向右平移n(n>0)个单位,同时将该二次函数在2≤x≤7的部分向左平移n个单位后得到的图象记为G,请结合图象直接回答,当图象G与平移后的线段有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
查看答案和解析>>
科目:初中数学 来源: 题型:
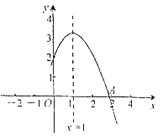
【题目】如图所示,二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的图象的一部分与
)的图象的一部分与![]() 轴的交点
轴的交点![]() 在
在![]() 与
与![]() 之间,对称轴为直线
之间,对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
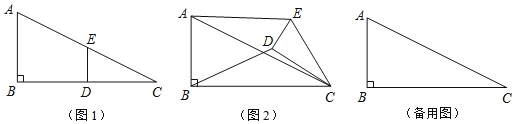
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(![]() ,0),与y轴的交点B在(0,0)和(0,﹣1)之间(不包括这两点),对称轴为直线x=
,0),与y轴的交点B在(0,0)和(0,﹣1)之间(不包括这两点),对称轴为直线x=![]() .则下列结论:① x>3时,y<0;② 4a+b<0;③﹣
.则下列结论:① x>3时,y<0;② 4a+b<0;③﹣![]() <a<0;④ 4ac+b2<4a.其中正确的是( )
<a<0;④ 4ac+b2<4a.其中正确的是( )
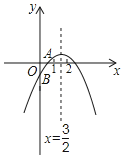
A.②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,线段
,线段![]() 、
、![]() 的长是一元二次方程
的长是一元二次方程![]() 的两根
的两根![]() ,
,![]() ,点
,点![]() 的横坐标为3,反比例函数
的横坐标为3,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
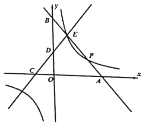
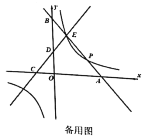
(1)若直线![]() 与反比例函数图象上除点
与反比例函数图象上除点![]() 外的另一交点为
外的另一交点为![]() ,求
,求![]() 的面积;若点
的面积;若点![]() 在
在![]() 轴上,若点
轴上,若点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值..
的最小值..
(2)若点![]() 在坐标轴上,在平面内是否存在一点
在坐标轴上,在平面内是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形且线段
为顶点的四边形是矩形且线段![]() 为矩形的一条边?若存在,直接写出符合条件的
为矩形的一条边?若存在,直接写出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com