
【题目】已知:如图,∠MON在∠AOB的内部,点C、D分别在射线OA、OB上,且OC=OD,CE⊥OA,DF⊥OB,分别交OM、ON于点E,F.
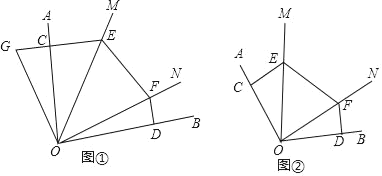
(1)如图①所示,若∠AOB=90°,∠MON=45°,延长EC至点G,使得CG=DF.请证明EF=CE+DF;
(2)如图②所示,若∠AOB=115°,EF=CE+DF,求∠MON的度数?
【答案】(1)详见解析;(2)∠MON=57.5°
【解析】
(1)先证出△OCG≌△ODF(SAS),再证出△EOG≌△EOF(SAS),即可得:EF=CE+DF;
(2)仿照(1)的思路,延长EC至G,使CG=DF,连接OG,先证明:△OCG≌△ODF(SAS),再证明:△OEG≌△OEF(SSS),即可求得:∠MON=57.5°.
解:(1)如图①,
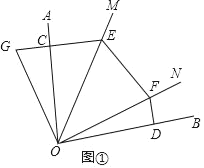
证明:∵CE⊥OA,DF⊥OB,
∴∠OCG=∠ODF=90°,
∵OC=OD,CG=DF.
∴△OCG≌△ODF(SAS)
∴∠COG=∠DOF,OG=OF
∵∠AOB=90°,∠MON=45°,
∴∠COE+∠DOF=45°
∴∠COE+∠COG=45°
即∠EOG=45°=∠MON
在△EOG≌△EOF中
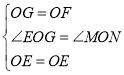
∴△EOG≌△EOF(SAS)
∴EF=EG
即:EF=CE+DF.
(2)如图②,延长EC至G,使CG=DF,连接OG,
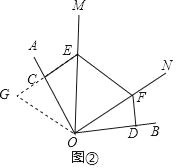
∵CE⊥OA,DF⊥OB,
∴∠OCG=∠ODF=90°,
∵OC=OD,CG=DF.
∴△OCG≌△ODF(SAS)
∴∠COG=∠DOF,OG=OF
∵EG=CE+CG=CE+DF,EF=CE+DF,
∴EG=EF
∵OE=OE
∴△OEG≌△OEF(SSS)
∴∠EOG=∠EOF
∵∠EOG+∠EOF=∠COG+∠AOF=∠DOF+∠AOF=∠AOB=115°
∴∠EOF=![]() ∠AOB=57.5°
∠AOB=57.5°
即:∠MON=57.5°


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
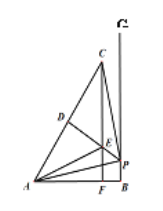
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,连接AP,作AP⊥CP且AP=CP,连接AC,PD平分∠APC,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,连接CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=mx+n与反比例函数交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1) 若m=k,n=0,求A,B两点的坐标(用m表示).
(2) 如图1,若A(x1,y1)、B(x2,y2),写出y1+y2与n的大小关系,并证明.
(3) 如图2,M、N分别为反比例函数![]() 图象上的点,AM∥BN∥x轴.若
图象上的点,AM∥BN∥x轴.若![]() ,且AM,BN之间的距离为5,则k-b=_____________
,且AM,BN之间的距离为5,则k-b=_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点P在函数![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
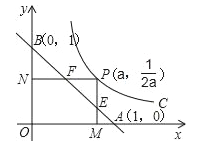
A. 4 B. 2 C. 1 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com