
【题目】如图,在△ABC中,AC=CB,O是AB的中点,CA与⊙O相切于点E,CO交⊙O于点D
(1)求证:CB是⊙O的切线;
(2)若∠ACB=80°,点P是⊙O上一个动点(不与D,E两点重合),求∠DPE的度数.
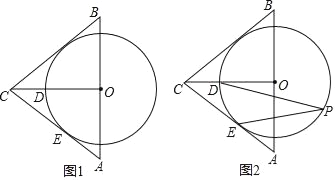
【答案】(1)详见解析;(2)∠DPE的度数为25°或155°.
【解析】
(1)经过半径的外端且垂直于这条半径的直线是圆的切线,据此进行判断.
(2)依据∠ACB=80°,OC平分∠ACB,可得∠ACO=40°,∠DOE=90°-40°=50°,分两种情况:当点P在优弧弧DPE上时,∠DPE=![]() ∠DOE=25°;当点P在劣弧弧DE上时,∠DPE=180°-25°=155°.
∠DOE=25°;当点P在劣弧弧DE上时,∠DPE=180°-25°=155°.
解:(1)如图1所示,连接OE,过O作OF⊥BC于F,
∵CA与⊙O相切于点E,
∴OE⊥AC,
∵△ABC中,AC=CB,O是AB的中点,
∴OC平分∠ACB,
∴OE=OF,
又∵OE是⊙O的半径,
∴CB是⊙O的切线;
(2)如图2,∵∠ACB=80°,OC平分∠ACB,
∴∠ACO=40°,
又∵OE⊥AC,
∴∠DOE=90°﹣40°=50°,
当点P在优弧![]() 上时,∠DPE=
上时,∠DPE=![]() ∠DOE=25°;
∠DOE=25°;
当点P在劣弧![]() 上时,∠DPE=180°﹣25°=155°.
上时,∠DPE=180°﹣25°=155°.
∴∠DPE的度数为25°或155°.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线![]() 与反比例函数
与反比例函数![]() (k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在∠AOB的内部求作点P,使点P到∠AOB的两边OA、OB的距离相等,且PA=PB;再写出点P的坐标.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() (k为常数).
(k为常数).
(1)若抛物线经过点(1,k2),求k的值;
(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;
(3)若将抛物线向右平移1个单位长度得到新抛物线,当1≤x≤2时,新抛物线对应的函数有最小值![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
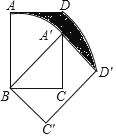
【题目】如图,在矩形ABCD中AB=![]() ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
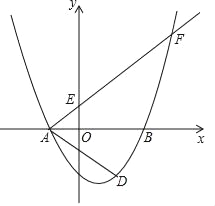
【题目】如图,在平面直角坐标系xOy中,已知抛物线y= ![]() 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且![]() .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
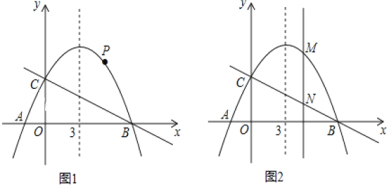
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com