
【题目】已知二次函数的解析式是y=x2﹣2x﹣3
(1)用配方法将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)在直角坐标系中,用五点法画出它的图象;
(3)利用图象求当x为何值时,函数值y<0
(4)当x为何值时,y随x的增大而减小?
(5)当﹣3<x<3时,观察图象直接写出函数值y的取值的范围.

【答案】(1)y=(x﹣1)2﹣4;(2)见试题解析;(3)由图象知,当﹣1<x<3时,函数值y<0;
(4)由图象知,当x<1时,y随x的增大而减小;
(5)当x=﹣3时,y=9+6﹣3=12,则﹣3<x<3时,0<y<12.
【解析】
试题分析:(1)利用配方法将函数解析式进行转换即可;
(2)根据顶点式求得顶点坐标,令x=0,求得与y轴的交点,令y=0,求得与x轴的坐标,再在对称轴的两侧取两组对称点,列表,然后描点、连线即可.
(3)、(4)、(5)根据二次函数图象的性质即可解答.
试题解析:(1)y=x2﹣2x﹣3=(x﹣1)2﹣4,即y=(x﹣1)2﹣4;
(2)由(1)可知,y=(x﹣1)2﹣4,则顶点坐标为(1,﹣4),
令x=0,则y=﹣3,
∴与y轴交点为(0,﹣3),
令y=0,则0=x2﹣2x﹣3,解得x1=﹣1,x2=3,
∴与x轴交点为(﹣1,0),(3,0).
列表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=x2﹣2x﹣3 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
描点、连线:
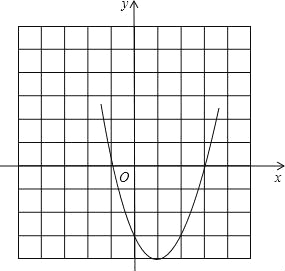
(3)由图象知,当﹣1<x<3时,函数值y<0;
(4)由图象知,当x<1时,y随x的增大而减小;
(5)当x=﹣3时,y=9+6﹣3=12,则﹣3<x<3时,0<y<12.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)(+26)﹣(﹣26)﹣6
(2)(﹣4)× ![]() ÷8
÷8
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)(﹣2)2﹣[﹣32+(﹣11)]×(﹣2)÷(﹣1)2016 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣1)
C.(﹣1,﹣2)
D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个仓库要向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)(本题满分10分)
路程/千米 | 运费(元/吨、千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A地 | 20 | 15 | 12 | 12 |
B地 | 25 | 20 | 10 | 8 |
(1)设甲库运往A地水泥![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
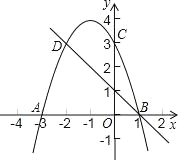
【题目】如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的对应点位置如图所示 ![]()
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ ![]() |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求 ![]() +
+ ![]() ﹣
﹣ ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com