
【题目】2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
【答案】(1)这组样本数据的平均数是15.1,众数为l0, 中位数为l2.5; (2)可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.
【解析】
(1)先根据表格提示的数据求出50名学生的捐款总金额,然后除以50即可求出平均数,在这组样本数据中,10出现的次数最多,所以求出了众数,将这组样本数据按从小到大的顺序排列,其中处于中间的两个数是10,15,从而求出中位数是,12.5;
(2)从表格中得知在50名学生中,捐款多于15元的学生有15名,所以可以估计该校九年级300名学生在本次活动中捐款多于15元的人数为300×![]() =90.
=90.
(1)观察表格,可知这组样本数据的平均数是![]() =15.1;
=15.1;
∴这组样本数据的平均数是15.1.
在这组样本数据中,10出现了18次,出现的次数最多,
∴这组样本数据的众数为l0.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数分别是10,15,
∴这组数据的中位数为l2.5.
(2)在50名学生中,捐款多于15元的学生有15名,有300×![]() =90(名).
=90(名).
∴根据样本数据,可以估计该校九年级300名学生在本次活动中捐款多于15元的约有90名.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生组织甲、乙两个旅行团去某景点旅游,已知甲团人数少于50人,乙团人数不超过100人.下面是小明与其他两位同学交流的情况.根据他们的对话,组织者算了一下,若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.



(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组利用大小不等、颜色各异的正方形硬纸片开展了一次活动,请认真阅读下面的探究片段,完成所提出的问题。
探究1:四边形ABCD是边长为1正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,小明看到图(1)后,很快发现AE=EF,这需要证明AE与EF所在的两个三角形全等,但△ABE与△FCE显然不全等,考虑到点E是BC的中点,引条辅助线尝试就行了,随即小明写出了如下的证明过程:证明:取AB的中点H,连接EH,证明△AHE与△ECF全等即可.
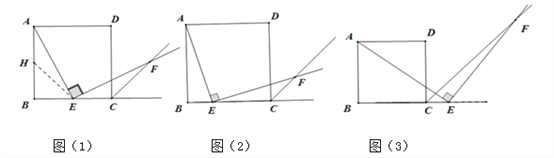
探究2:小明继续探索,把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,如图(2)其它条件不变,结论AE=EF是否成立呢? (填是或否)
小明还想试试,把条件“点E是边BC的中点”改为“点E是边BC延长线上的任意一点”,如图(3)其它条件不变,那么结论AE=EF是否还成立呢? (填是或否),请你选择其中一种完成证明过程给小强看。
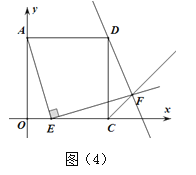
探究3:在探究2结论AE=EF成立的情况下,如图(4)所示的平面直角坐标系中,当点E滑动到BC上某处时(不含B、C),点F恰好落在直线y=-2x+3上,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
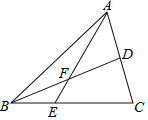
【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一组数据x1,x2,…,xn中,各数据与它们的平均数![]() 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T=![]() (|x1-
(|x1-![]() |+|x2-
|+|x2-![]() |+…+|xn-
|+…+|xn-![]() |)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
一水产养殖户李大爷要了解鱼塘中鱼的质量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况.为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度的几个量中某些值超标时就要捕捞,分开养殖或出售.他从甲、乙两个鱼塘各随机捕捞10条鱼称得质量(单位:千克)如下:
甲鱼塘:3、5、5、5、7、7、5、5、5、3
乙鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算从甲、乙两个鱼塘中抽取的10条鱼的质量的极差(极差:最大值与最小值的差)、方差、平均差.完成下面的表格:
极差(千克) | 方差 | 平均差(千克) | |
甲鱼塘 | |||
乙鱼塘 |
(2)如果你是技术人员,你会告诉李大爷哪个鱼塘的风险更大些?哪些量更能说明鱼质量的离散程度?
查看答案和解析>>
科目:初中数学 来源: 题型:
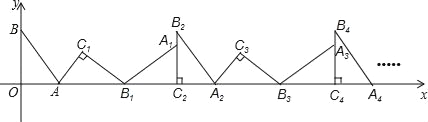
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com