
【题目】在一组数据x1,x2,…,xn中,各数据与它们的平均数![]() 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T=![]() (|x1-
(|x1-![]() |+|x2-
|+|x2-![]() |+…+|xn-
|+…+|xn-![]() |)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
一水产养殖户李大爷要了解鱼塘中鱼的质量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况.为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度的几个量中某些值超标时就要捕捞,分开养殖或出售.他从甲、乙两个鱼塘各随机捕捞10条鱼称得质量(单位:千克)如下:
甲鱼塘:3、5、5、5、7、7、5、5、5、3
乙鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算从甲、乙两个鱼塘中抽取的10条鱼的质量的极差(极差:最大值与最小值的差)、方差、平均差.完成下面的表格:
极差(千克) | 方差 | 平均差(千克) | |
甲鱼塘 | |||
乙鱼塘 |
(2)如果你是技术人员,你会告诉李大爷哪个鱼塘的风险更大些?哪些量更能说明鱼质量的离散程度?
【答案】(1)(6分)
极差 | 方差 | 平均差 | |
A | 4 | 1.6 | 0.8 |
B | 2 | 0.8 | 0.8 |
(2)极差与方差 (4分)
【解析】
试题(1)根据极差、方差、平均差的定义分别计算即可;(2)因为要防止出现“大鱼吃小鱼”的情况,所以注意了解鱼塘中鱼的重量的离散程度,即波动大小,波动大的风险更大,根据(1)中的数据可得极差与方差更能说明鱼重量的离散程度.
试题解析:(1)甲组数据中最大的值7,最小值3,故极差=7-3=4,
![]() 甲=(3×2+6×5+2×7)÷10=5,S2甲=
甲=(3×2+6×5+2×7)÷10=5,S2甲=![]() =1.6,
=1.6,
![]() =
=![]() (|3-5|+|5-5|+…+|3-5|)=0.8;
(|3-5|+|5-5|+…+|3-5|)=0.8;
乙组数据中最大的值6,最小值4,故极差=6-4=2;乙=(4×4+6×4+5×2)÷10=5,
![]() =
=![]() (|4-5|+|4-5|+…+|4-5|)=0.8;
(|4-5|+|4-5|+…+|4-5|)=0.8;
S2乙=[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2+(5-5)2+(6-5)2+(6-5)2+(4-5)2+(4-5)2]÷10=0.8,
极差 | 方差 | 平均差 | |
A | 4 | 1.6 | 0.8 |
B | 2 | 0.8 | 0.8 |
(2)∵S2甲<S2乙;所以根据A,B的极差与方差可以得出A鱼塘风险更大.极差与方差更能说明鱼重量的离散程度


科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.
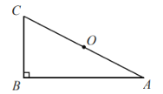
求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规,在图中补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°,
∴![]() ABCD为矩形(_________)(填推理的依据).
ABCD为矩形(_________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果等腰三角形一腰上的高与另一腰的夹角45°,那么这个等腰三角形的底角为( )
A. 67°50′B. 22°C. 67.5°D. 22.5°或67.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
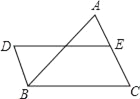
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:BC=DE;
(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,![]() 分裂后第一个数是____________(用含m的代数式表示);若
分裂后第一个数是____________(用含m的代数式表示);若![]() 分裂后,其中有一个奇数是2019,则m的值是_________.
分裂后,其中有一个奇数是2019,则m的值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com