
【题目】某数学兴趣小组利用大小不等、颜色各异的正方形硬纸片开展了一次活动,请认真阅读下面的探究片段,完成所提出的问题。
探究1:四边形ABCD是边长为1正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,小明看到图(1)后,很快发现AE=EF,这需要证明AE与EF所在的两个三角形全等,但△ABE与△FCE显然不全等,考虑到点E是BC的中点,引条辅助线尝试就行了,随即小明写出了如下的证明过程:证明:取AB的中点H,连接EH,证明△AHE与△ECF全等即可.
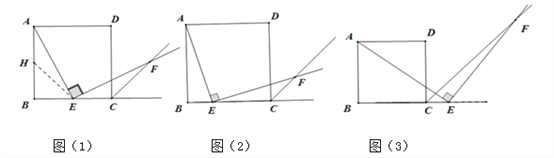
探究2:小明继续探索,把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,如图(2)其它条件不变,结论AE=EF是否成立呢? (填是或否)
小明还想试试,把条件“点E是边BC的中点”改为“点E是边BC延长线上的任意一点”,如图(3)其它条件不变,那么结论AE=EF是否还成立呢? (填是或否),请你选择其中一种完成证明过程给小强看。
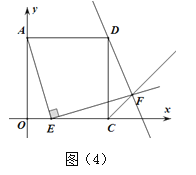
探究3:在探究2结论AE=EF成立的情况下,如图(4)所示的平面直角坐标系中,当点E滑动到BC上某处时(不含B、C),点F恰好落在直线y=-2x+3上,求此时点F的坐标.
【答案】 (1)见解析;(2) F(![]() ,
,![]() ).
).
【解析】分析:探究1:取AB的中点H,连接EH,根据同角的余角相等得到∠BAE=∠CEF,证明△HAE≌△CEF即可;
探究2:①在AB上取点P,连接EP,同(1)的方法相似,证明△PAE≌△CEF即可;
②延长BA至H,使AH=CE,连接HE,证明△HAE≌△CEF即可.
探究3:设F(a,﹣2a+3),过F作FH⊥x轴于H,作FG⊥CD于G,如图4,只要证明FG=FH,由此构建方程即可解决问题;
详解:探究1:如图1,取AB的中点H,连接EH.
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°.
∵AH=EC,∴BH=BE,∴∠BHE=45°,∠AHE=135°.
∵CF是正方形外角的平分线,∴∠ECF=135°.
∵∠AEF=90°,∠B=90°,∴∠BAE=∠CEF.
在△HAE和△CEF中,∵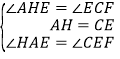 ,∴△HAE≌△CEF,∴AE=EF;
,∴△HAE≌△CEF,∴AE=EF;
探究2:①结论:是.
理由:如图2,在AB上取点P,连接EP.
∵四边形ABCD是正方形,∴AB=BC,∠B=∠BCD=90°.
∵AP=EC,∴BP=BE,∴∠BPE=45°,∠APE=135°.
∵CF是正方形外角的平分线,∴∠ECF=135°.
∵∠AEF=90°,∠B=90°,∴∠BAE=∠CEF.在△PAE和△CEF中,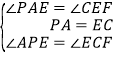 ,∴△PAE≌△CEF,∴AE=EF;
,∴△PAE≌△CEF,∴AE=EF;
②结论:是.
理由:如图3,延长BA至H,使AH=CE,连接HE.
∵BA=BC,AH=CE,∴BH=BE,∴∠H=45°.
∵CF是正方形外角的平分线,∴∠ECF=45°,∴∠H=∠ECF.
∵∠AEF=90°,∠B=90°,∠HAE=∠B+∠BEA,∠CEF=∠AEF+∠BEA,
∴∠HAE=∠CEF.
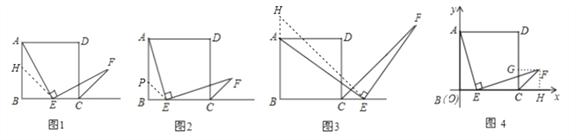
在△HAE和△CEF中,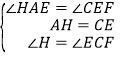 ,∴△HAE≌△CEF,∴AE=EF.
,∴△HAE≌△CEF,∴AE=EF.
探究3:②设F(a,﹣2a+3),过F作FH⊥x轴于H,作FG⊥CD于G,如图4,
则CH=a﹣1,FH=﹣2a+3.
∵CF为角平分线,∴FH=CH,∴a﹣1=﹣2a+3,解得:a=![]() .当a=
.当a=![]() 时,﹣2a+3=﹣2×
时,﹣2a+3=﹣2×![]() +3=
+3=![]() ,∴F点坐标为(
,∴F点坐标为(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.点P从点A出发,沿AC以每秒1个单位的速度向终点C运动;点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动.当点P停止运动时,点Q也随之停止.点P、Q同时出发,设点P的运动时间为t(秒).
(1)求AB的长.
(2)用含t的代数式表示CP的长.
(3)设点Q到CA的距离为y,求y与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
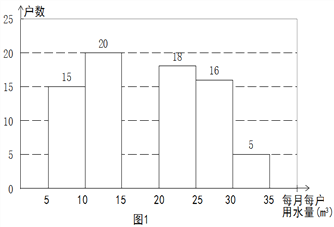
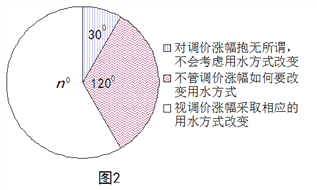
小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n =________,小明调查了_____户居民,并补全图1;
(2)每月每户用水量的中位数落在______之间,众数落在_______之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
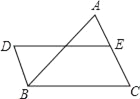
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
(1)求证:BC=DE;
(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com