
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 是
是![]() 与
与![]() 三等分线的交点,连接
三等分线的交点,连接![]()

(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)50°.
【解析】
(1)过点N作NG⊥BC于G,NE⊥BM于E,FN⊥CM于F,根据角平分线上的点到角的两边的距离相等可得FG=FM=FN,再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC
(2)根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角的三等分求出∠EBC+∠ECB的度数,然后利用三角形内角和定理求出∠BEC的度数,从而得解
(1)如图,过点N作NG⊥BC于G,NE⊥BM于E,FN⊥CM于F,
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M,N,
∴BN平分∠MBC,CN平分∠MCB,
∴CN=EN,CN=FN,
∴EN=FN,
∴![]() 平分
平分![]() ;
;
(2)∵![]() 平分
平分![]() ;
;
∴∠BMN=![]() ∠BMC,
∠BMC,
∵∠A=60,
∴∠ABC+∠ACB=180°∠A=180°60°=120°
根据三等分,∠MBC+∠MCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×120°=80°
×120°=80°
在△BMC中,∠BMC=180°(∠MBC+∠MCB)=180°80°=100°
∴![]() =
=![]() ×100°=50°
×100°=50°



 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
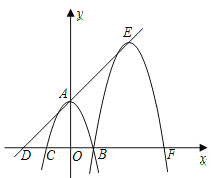
【题目】如图,在平面直角坐标系xoy中,二次函数![]() (
(![]() )的图象经过A(0,4),B(2,0),C(-2,0)三点.
)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的解析式;
(2)在x轴上有一点D(-4,0),将二次函数图象沿DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②求图象A,B两点间的部分扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东40°方向航行,“海天”号以每小时12海里的速度向北偏西一定的角度的航向行驶,它们离港口一个半小时后分别位于Q、R处,且相距30海里(即RQ=30).解答下列问题:
(1)求PR、PQ的值;
(2)求“海天”号航行的方向.(即求北偏西多少度?)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x、y的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求![]() 的取值范围;
的取值范围;
(2)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:

第4个图案中有白色纸片________块,第n个图案中有白色纸片________块。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=kx+b,当-1≤x≤4时,3≤y≤6,则k,b的值分别是______________.点M(a-1,2-a)不在第________ 象限.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com