
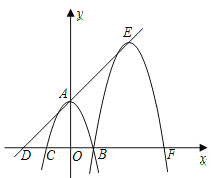
【题目】如图,在平面直角坐标系xoy中,二次函数![]() (
(![]() )的图象经过A(0,4),B(2,0),C(-2,0)三点.
)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的解析式;
(2)在x轴上有一点D(-4,0),将二次函数图象沿DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②求图象A,B两点间的部分扫过的面积.
【答案】(1)y=-x2+4;(2) E(5,9);(3)30.
【解析】试题分析: ![]() 用待定系数法即可求得二次函数解析式.
用待定系数法即可求得二次函数解析式.
![]() ①求出直线DA的解析式,设E(m,m+4),根据顶点式写出平移之后的二次函数解析式
①求出直线DA的解析式,设E(m,m+4),根据顶点式写出平移之后的二次函数解析式![]() .把点
.把点![]() 的坐标代入求出
的坐标代入求出![]() 的值,即可求出顶点E的坐标.
的值,即可求出顶点E的坐标.
②连接AB,过点B作BL∥AD交平移后的抛物线于点G,连结EG,四边形ABGE的面积就是图象A,B两点间的部分扫过的面积.求出四边形的面积即可.
试题解析:
(1)把![]() 代入
代入![]() ,得
,得
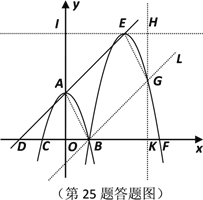
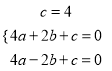 ,
,
解得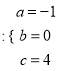 ,
,
![]() .
.
(2)①设直线DA的解析式为y=kx+d(k≠0),
把A(0,4),D(-4,0)代入得,
![]() ,
,
解得: ![]() ,
,
∴y=x+4,
设E(m,m+4),
平移后的抛物线的解析式为: ![]() .
.
把B(2,0)代入得: ![]()
解得: ![]() 舍去,
舍去,
∴E(5,9).
②如图,连接AB,过点B作BL∥AD交平移后的抛物线于点G,连结EG,
∴四边形ABGE的面积就是图象A,B两点间的部分扫过的面积.
过点G作GK⊥x轴于点K,过点E作EI⊥y轴于点I,直线EI,GK交于点H.
由点A(0,4)平移至点E(5,9),可知点B先向右平移5个单位,再向上平移5个单位至点G.
∵B(2,0),∴点G(7,5),
∴GK=5,OB=2,OK=7,
∴BK=OK-OB=7-2=5,
∵A(0,4),E(5,9),
∴AI=9-4=5,EI=5,
∴EH=7-5=2,HG=9-5=4,
∴S四边形ABGH=S矩形IOKH![]()
![]()
答:图象A,B两点间的部分扫过的面积为30.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,垂足为D.
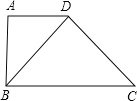
(1)若AD=9,BC=16,求BD的长;
(2)求证:AB2BC=CD2AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
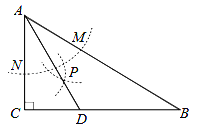
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①![]() 是
是![]() 的平分线;②
的平分线;②![]() ;③
;③![]() ;④
;④![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格规定如表:
购票人数 | 1-50人 | 51-100人 | 100人以上 |
票价 | 10元/人 | 8元/人 | 5元/人 |
(1)某校七年组甲、乙两班共100多人去该公园举行联欢活动,其中甲班50多人,乙班不足50人,如果以班为单位分别买票,两个班一共应付920元;如果两个班联合起一作为一团体购票,一共只要付515元.问:甲、乙两班分别有多少人?
(2)若有![]() 两个团队共160人,以各自团队为单位分别买票,共用950元,问
两个团队共160人,以各自团队为单位分别买票,共用950元,问![]() 两个团队各有多少人?
两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米) | … | 1.80~1.86 | 1.86~1.94 | 1.94~2.02 | 2.02~2.18 | 2.18~2.34 | 2.34~ |
得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有________.(填上所有正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com