
【题目】如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有________.(填上所有正确结论的序号)

【答案】①②③④
【解析】
连接![]() ,证明
,证明![]() ,利用等腰三角形的性质可判断结论①;由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO与∠DCO的和等于30°,再证明
,利用等腰三角形的性质可判断结论①;由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO与∠DCO的和等于30°,再证明![]() 是等边三角形,可判断结论②,③;, 在线段AC上截取AE=AP,连接PE,证明△APO≌△EPC可判断结论④.
是等边三角形,可判断结论②,③;, 在线段AC上截取AE=AP,连接PE,证明△APO≌△EPC可判断结论④.
解:如图,连接![]()
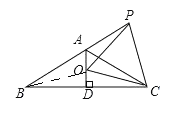
∵AD⊥BC,![]()
![]() 是
是![]() 的中垂线,
的中垂线,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即结论①正确;
即结论①正确;
连接BO,如图1所示:
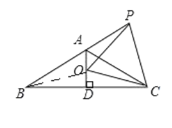
![]()
![]()
由![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
![]()
即结论②正确;
![]() 是等边三角形,
是等边三角形,
![]()
即结论③正确;
在线段AC上截取AE=AP,连接PE,如图所示:
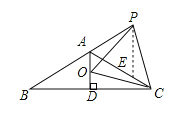
∵∠BAC+∠CAP=180°,∠BAC=120°,
∴∠CAP=60°,
∴△APE是等边三角形,
∴AP=EP,
又∵△OPC是等边三角形,
∴OP=CP,
又∵∠APE=∠APO+∠OPE=60°,
∠CPO=∠CPE+∠OPE=60°,
∴∠APO=∠EPC,
在△APO和△EPC中,
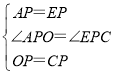 ,
,
∴△APO≌△EPC(SAS),
∴AO=EC,
又∵AC=AE+EC,AE=AP,
∴AC=AO+AP, 即结论④正确;
综合所述,①,②,③,④都正确,
故答案为:①,②,③,④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校教职工为庆祝“建国![]() 周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
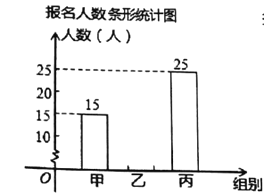
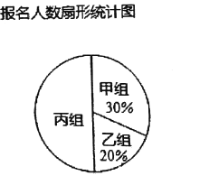
(1)该校教师报名参加本次学习强国知识竞赛的总人数为___________人,并补全条形统计图;
(2)该校教师报名参加丙组的人数所占圆心角度数是__________;
(3)根据实际情况,需从甲组抽调部分教师到丙组,使丙组人数是甲组人数的![]() 倍,应从甲组抽调多少名教师到丙组?
倍,应从甲组抽调多少名教师到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,二次函数![]() (
(![]() )的图象经过A(0,4),B(2,0),C(-2,0)三点.
)的图象经过A(0,4),B(2,0),C(-2,0)三点.
(1)求二次函数的解析式;
(2)在x轴上有一点D(-4,0),将二次函数图象沿DA方向平移,使图象再次经过点B.
①求平移后图象顶点E的坐标;
②求图象A,B两点间的部分扫过的面积.
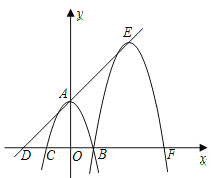
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买![]() 张办公桌必须买两把椅子,椅子每把
张办公桌必须买两把椅子,椅子每把![]() 元.若学校购买
元.若学校购买![]() 张甲种办公桌和
张甲种办公桌和![]() 张乙种办公桌共花费
张乙种办公桌共花费![]() 元,购买
元,购买![]() 张甲种办公桌比购买
张甲种办公桌比购买![]() 张乙种办公桌多花费
张乙种办公桌多花费![]() 元。
元。
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校准备用不超过![]() 元购买甲、乙两种办公桌共
元购买甲、乙两种办公桌共![]() 张,且甲种办公桌数量不多于乙种办公桌数量的
张,且甲种办公桌数量不多于乙种办公桌数量的![]() 倍,请求出有哪几种购买方案?
倍,请求出有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间![]() 用t表示,单位:小时
用t表示,单位:小时![]() ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

![]() 求本次调查的学生人数;
求本次调查的学生人数;
![]() 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
![]() 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]() .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东40°方向航行,“海天”号以每小时12海里的速度向北偏西一定的角度的航向行驶,它们离港口一个半小时后分别位于Q、R处,且相距30海里(即RQ=30).解答下列问题:
(1)求PR、PQ的值;
(2)求“海天”号航行的方向.(即求北偏西多少度?)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=kx+b,当-1≤x≤4时,3≤y≤6,则k,b的值分别是______________.点M(a-1,2-a)不在第________ 象限.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com