
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是弧AB上的—个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )

A.1 B.2 C. D.
D.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年辽宁省大石桥市八年级上学期段测数学试卷(解析版) 题型:填空题
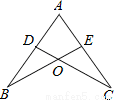
如图,点D、E分别在线段AB、AC上,BE、CD相交于点O,AE=AD要使△ABE≌△ACD,需添加一个条件是 (只要写一个条件).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:解答题
有背面一样,正面分别是2、3、4、5的4张扑克牌.两次随机摸一张牌看正面的点数(每一次摸牌后放回).
(1)通过画树状图或列表,列举出所有点数之和的所有可能结果;
(2)求点数之和不超过6的概率P.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:填空题
若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:解答题
平面直角坐标系中,如图,将 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。

(1)当n=1时,如果a=-1,试求b的值。
(2)当n=2时,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式。
(3)当n=3时,将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O,求a的值。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:解答题
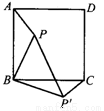
如图,P是正方形内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若BP=3,求PP′.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
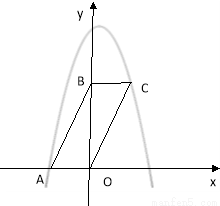
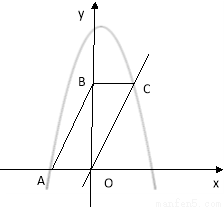
(14分)如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线 经过点A和C.
经过点A和C.
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为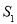 ,右侧部分图形的面积记为
,右侧部分图形的面积记为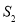 ,求
,求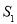 与
与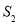 的比.
的比.
(3)在y轴上取一点D,坐标是(0, ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到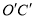 ,点D关于直线
,点D关于直线 的对称点记为
的对称点记为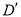 ,当点
,当点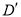 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点 坐标并直接写出直线
坐标并直接写出直线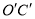 的函数解析式.
的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com