
【题目】如图,平行四边形![]() 的对角线
的对角线![]() 、
、![]() 相交于点O,
相交于点O,![]() .
.
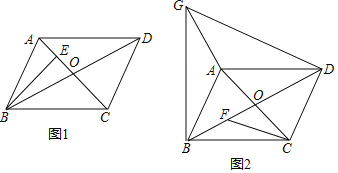
(1)如图1,过B作![]() 于E,若
于E,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,过点C作
,过点C作![]() 交
交![]() 于点F,过点B作
于点F,过点B作![]() 且
且![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
【答案】(1)![]() -4;(2)见解析.
-4;(2)见解析.
【解析】
(1)由勾股定理可求CE的长,由平行四边形的性质可得CO的长,即可求OE的长;
(2)延长CF交AB于点H,由“SAS”可证△ABG≌△FCB,可得AG=BF,由等腰三角形的性质可得AB=CD=2BH,再证明三角形BFH为等腰直角三角形,从而得出BF=![]() BH①;在Rt△CDF中,得出DF=
BH①;在Rt△CDF中,得出DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,继而得出OF=BO-BF=
BH,继而得出OF=BO-BF=![]() BH②,结合①②可得出结论.
BH②,结合①②可得出结论.
(1)解:∵BC=AC=8,BE=5,![]() ,
,
∴CE=![]() .
.
∵四边形ABCD是平行四边形,
∴AO=CO=4,
∴OE=EC-OC=![]() -4;
-4;
(2)证明:如图,延长CF交AB于点H,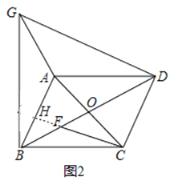
∵CF⊥CD,∠BDC=45°,
∴∠BDC=∠DFC=45°,
∴∠FBC+∠FCB=45°,CF=CD,
∵BC⊥BG,∠ABD=∠BDC=45°,
∴∠GBA+∠FBC=45°,
∴∠ABG=∠BCF,且AB=CD=CF,BC=BG,
∴△ABG≌△FCB(SAS),
∴AG=BF.
∵∠ABG+∠ABC=90°,∴∠BCF+∠ABC=90°,
∴CH⊥AB,又AC=BC,∴BH=AH,∴AB=CD=2BH.
∵AB∥CD,
∴∠ABF=∠CDB=45°,
∴∠HBF=∠BFH=45°,∴BH=FH,
∴BF=![]() BH①.
BH①.
在Rt△CDF中,CD=CF,∴DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,
BH,
∴BD=BF+DF=![]() BH +2
BH +2![]() BH=3
BH=3![]() BH,
BH,
∴BO=![]() BD=
BD=![]() BH,
BH,
∴OF=BO-BF=![]() BH②,
BH②,
∴由①②得,BF=2OF,
∴AG=2OF.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1/s,设P,Q出发t秒时,△BPQ的面积为y,已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论::①AD=BE=5;②当0<t≤5时; ![]() ;③直线NH的解析式为y=-
;③直线NH的解析式为y=-![]() t+27;④若△ABE与△QBP相似,则t=
t+27;④若△ABE与△QBP相似,则t=![]() 秒. 其中正确的结论个数为( )
秒. 其中正确的结论个数为( )


A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
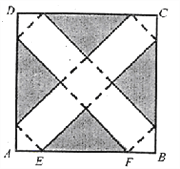
查看答案和解析>>
科目:初中数学 来源: 题型:
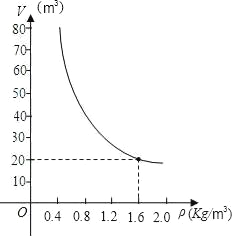
【题目】已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
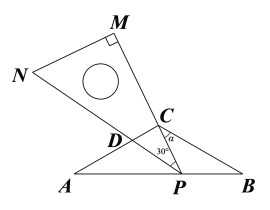
【题目】在△ABC中,CA=CB=3,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由.
(2)在点P滑动的过程中,当AP长度为多少时,△ADP≌△BPC,为什么?
(3)在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请直接写出α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
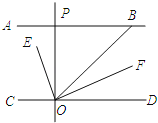
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有_____填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com