
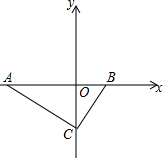
 ��ͼ����ƽ��ֱ������ϵ�У���A��x��ĸ������ϣ���B��x����������ϣ�C��y��ĸ������ϣ�AC����ֱ��Ϊy=kx-12��AC��BC��BC�ij���$\frac{1}{3}$���Ƿ���x2-3x-10=0�ĸ���
��ͼ����ƽ��ֱ������ϵ�У���A��x��ĸ������ϣ���B��x����������ϣ�C��y��ĸ������ϣ�AC����ֱ��Ϊy=kx-12��AC��BC��BC�ij���$\frac{1}{3}$���Ƿ���x2-3x-10=0�ĸ������� ��1�����Ƚⷽ����÷��̵Ľ⣬��BC�ij��ȼ�����ã�Ȼ��֤����AOC�ס�COB���������������εĶ�Ӧ�ߵı���ȼ������OA�ij�����A�����꼴����ã�
��2��ֱ��L������C��ƽ�֡�AOC���������ֱ��һ������OA���е㣬���ô���ϵ����������⣻
��3���ֳ��ı���ACPD�����κ��ı���APCD��������������������ۣ����ı���ACPD������ʱ���������AC�Ľ���ʽ������AC��PD�������PD�Ľ���ʽ����P�����꼴����ã�ͬ������ı���APCD������ʱP�����꣮
��� �⣺��1���ⷽ��x2-3x-10=0��x1=5��x2=-2��
��BC=3��5=15��
��y=kx-12�У���x=0�����y=-12����C�������ǣ�0��-12����OC=12��
��ֱ�ǡ�BOC�У�OB=$\sqrt{B{C}^{2}-O{C}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9����B�������ǣ�0��9����
�ߡ�ACB=90�㣬����ACO+��BCO=90�㣬
�֡�ֱ�ǡ�AOC�У���ACO+��CAO=90�㣬
���BCO=��CAO��
�֡ߡ�AOC=��BOC��
���AOC�ס�COB��
��$\frac{OA}{OC}$=$\frac{OC}{OB}$��
��$\frac{OA}{12}$=$\frac{12}{9}$��
��ã�OA=16��
��A�������ǣ�-16��0����
��2��OA���е�D�ǣ�-8��0����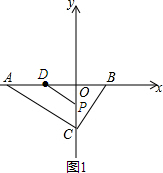
��ֱ��L�Ľ���ʽ��y=kx+b��
��������ã�$\left\{\begin{array}{l}{-8k+b=0}\\{b=-12}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=-12}\end{array}\right.$��
��ֱ��L�Ľ���ʽ��y=-$\frac{3}{2}$x-12��
��3�����ı���ACPD������ʱ����ͼ1��
��AC�Ľ���ʽ��y=mx+n�����������$\left\{\begin{array}{l}{-16m+n=0}\\{n=-12}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-\frac{3}{4}}\\{n=-12}\end{array}\right.$��
��ֱ��AC�Ľ���ʽ��y=-$\frac{3}{4}$x-12��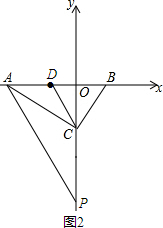
��DP�Ľ���ʽ��y=-$\frac{3}{4}$x+c����6+c=0��
��ã�c=-6��
��DP�Ľ���ʽ��y=-$\frac{3}{4}$x-6��
��x=0�����y=-6����P�������ǣ�0��-6����
���ı���APCD������ʱ����ͼ2��
ͬ����CD�Ľ���ʽ��y=-$\frac{3}{2}$x-12��
AP�Ľ���ʽ��y=-$\frac{3}{2}$x-24����P�������ǣ�0��-24����
��P�������ǣ�0��-6����0��-24����
���� ���⿼���˴���ϵ���������Ľ���ʽ���Լ����������ε��ж������ʣ���ȷ���������DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
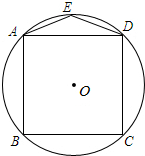 ��ͼ��������ABCD�ڽ��ڡ�O����E���ӻ�$\widehat{AD}$�ϣ����AED���ڣ�������
��ͼ��������ABCD�ڽ��ڡ�O����E���ӻ�$\widehat{AD}$�ϣ����AED���ڣ�������| A�� | 100�� | B�� | 120�� | C�� | 135�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
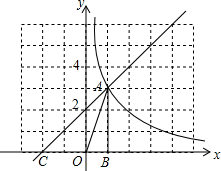 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+$\frac{1}{2}m$��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�һ�����ڽ��ڵ�A����x�ύ�ڵ�C��AB��ֱ��X�ᣬ����ΪB����������AOB�����Ϊ1��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+$\frac{1}{2}m$��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�һ�����ڽ��ڵ�A����x�ύ�ڵ�C��AB��ֱ��X�ᣬ����ΪB����������AOB�����Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
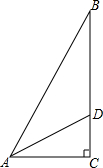 ��ͼ���ڡ�ABC�У���C=90�㣬��A��ƽ����AD=4����DAC=30�㣬��ֱ�ǡ�ABC��
��ͼ���ڡ�ABC�У���C=90�㣬��A��ƽ����AD=4����DAC=30�㣬��ֱ�ǡ�ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
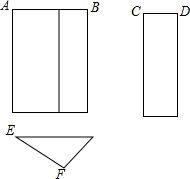 ��ͼ��һ��������������ͼ����AB=5��CD=2����EF�ij��Ȳ������ǣ�������
��ͼ��һ��������������ͼ����AB=5��CD=2����EF�ij��Ȳ������ǣ�������| A�� | 4 | B�� | 4.5 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
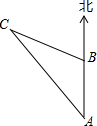 ��ͼ������8ʱ��һ���ִ���A��������ÿСʱ20������ٶ����������У�10ʱ����B�������ִ���A����õ���C�ڱ�ƫ��36�㣬���е�B��ʱ���ֲ�õ���C�ڱ�ƫ��72�㣬���B������C�ľ�����40���
��ͼ������8ʱ��һ���ִ���A��������ÿСʱ20������ٶ����������У�10ʱ����B�������ִ���A����õ���C�ڱ�ƫ��36�㣬���е�B��ʱ���ֲ�õ���C�ڱ�ƫ��72�㣬���B������C�ľ�����40����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com