
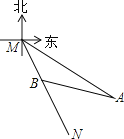
【题目】如图,射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为100海里.
(1)求点A到航线MN的距离;
(2)在航线MN上有一点B,且∠MAB=15°,若轮船的速度为50海里/时,求轮船从M处到B处所用时间为多少小时?(结果保留根号)
【答案】(1)点A到航线MN的距离为50海里;(2)轮船从M处到B处所用时间约为(![]() ﹣1)小时.
﹣1)小时.
【解析】
(1)过A作AH⊥MN于H.由方向角的定义可知∠QMB=30°,∠QMA=60°,那么∠NMA=∠QMA﹣∠QMB=30°.解直角△AMH中,得出AH=![]() AM,问题得解;
AM,问题得解;
(2)先根据直角三角形两锐角互余求出∠HAM=60°,由∠MAB=15°,得出∠HAB=∠HAM﹣∠MAB=45°,那么△AHB是等腰直角三角形,求出BH=AH距离,然后根据时间=路程÷速度即可求解.
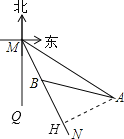
解:(1)如图,过A作AH⊥MN于H.
∵∠QMB=30°,∠QMA=60°,
∴∠NMA=∠QMA﹣∠QMB=30°.
在直角△AMH中,∵∠AHM=90°,∠AMH=30°,AM=100海里,
∴AH=![]() AM=50海里,
AM=50海里,
答:点A到航线MN的距离为50海里;
(2)在直角△AMH中,∵∠AHM=90°,∠AMH=30°,
∴∠HAM=60°,
∵∠MAB=15°,
∴∠HAB=∠HAM﹣∠MAB=45°,
∵∠AHB=90°,
∴BH=AH=50海里,
∵MH=![]() AH=50
AH=50![]() 海里,
海里,
∴MB=(50![]() ﹣50)海里,
﹣50)海里,
∴轮船从M处到B处所用时间为:![]() 小时,
小时,
答:轮船从M处到B处所用时间约为(![]() ﹣1)小时.
﹣1)小时.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
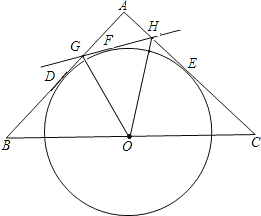
【题目】在Rt△ABC中,∠A=90°,AB=AC=4,O是BC边上的点且⊙O与AB、AC都相切,切点分别为D、E.
(1)求⊙O的半径;
(2)如果F为![]() 上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;
上的一个动点(不与D、E),过点F作⊙O的切线分别与边AB、AC相交于G、H,连接OG、OH,有两个结论:①四边形BCHG的周长不变,②∠GOH的度数不变.已知这两个结论只有一个正确,找出正确的结论并证明;
(3)探究:在(2)的条件下,设BG=x,CH=y,试问y与x之间满足怎样的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
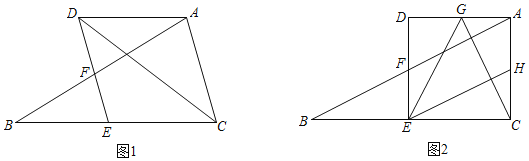
【题目】在△ABC中,过A作BC的平行线,交∠ACB的平分线于点D,点E是BC上一点,连接DE,交AB于点F,∠DEB+∠CAD=180°.
(1)如图1,求证:四边形ACED是菱形;
(2)如图2,G是AD的中点,H是AC边中点,连接CG、EG、EH,若∠ACB=90°,BC=2AC,在不添加任何辅助线的情况下,请直接写出图中与△CEH全等的三角形(不含△CEH本身).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,顶点
,顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴,抛物线
轴的正半轴,抛物线![]() 经过
经过![]() 两点,点
两点,点![]() 为抛物线的顶点,连接
为抛物线的顶点,连接![]() .
.
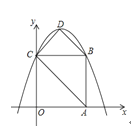
(1)求此抛物线的解析式;
(2)直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过圆外一点P作⊙O的两条切线,切点分别为A、B,连接AB,在AB、PB、PA上分别取一点D、E、F,使AD=BE,BD=AF,连接DE、DF、EF,则∠EDF等于( )
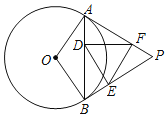
A.90°﹣∠PB.90°﹣![]() ∠PC.180°﹣∠PD.45°﹣
∠PC.180°﹣∠PD.45°﹣![]() ∠P
∠P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数图象过A,B,C三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.

(1)求点C的坐标;
(2)求二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,y随x的增大而增大,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,点M在直线y=﹣2x﹣3上,请验证点N也在y=﹣2x﹣3上并求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
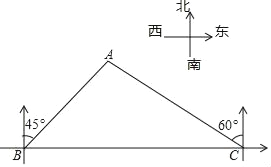
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com