
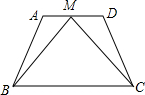
 已知:如图,AB=CD,∠A=∠D,点M是AD的中点.
已知:如图,AB=CD,∠A=∠D,点M是AD的中点.科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +4 | -2 | -3 | +15 | -12 | +21 | -14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
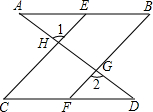 完成下面的证明过程:
完成下面的证明过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
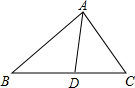 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )| A. | 3:4 | B. | 4:3 | C. | 16:9 | D. | 9:16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
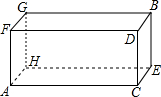 有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.
有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com