
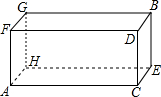
 有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.
有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线. 分析 分为三种情况展开,根据勾股定理求出线段AB的长度,再进行比较即可.
解答 解:①如图1,展开后连接AB,则AB就是在表面上A到B的最短距离,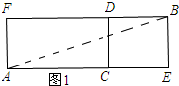
∠AEB=90°,AE=12+9=21,BE=7,
在Rt△AEB中,由勾股定理得:AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{2{1}^{2}+{7}^{2}}$=$\sqrt{490}$=7$\sqrt{10}$;
②如图2,展开后连接AB,则AB就是在表面上A到B的最短距离,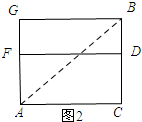
∠ACB=90°,AC=12,BC=9+7=16,
在Rt△ACB中,由勾股定理得:AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=$\sqrt{400}$=20;
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,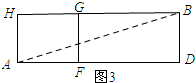
∠ADB=90°,AD=7+12=19,BD=9,
在Rt△ADB中,由勾股定理得:AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{1{9}^{2}+{9}^{2}}$=$\sqrt{442}$.
∵400<442<490,
∴20$<\sqrt{442}<\sqrt{490}$.
所以由A到B的最短路线为如2所示的路线.
点评 本题考查了平面展开-最短路线问题和勾股定理等知识点,关键是能画出展开图形并能求出符合条件的最短路线.


科目:初中数学 来源: 题型:解答题
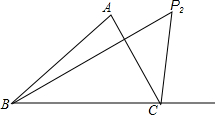 如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP2、CP2相交于点P2,∠P2BC=3∠ABP2,∠P2CD=3∠ACP2,直接写出∠A、∠P2之间满足的数量关系.
如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP2、CP2相交于点P2,∠P2BC=3∠ABP2,∠P2CD=3∠ACP2,直接写出∠A、∠P2之间满足的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com