
分析 (1)把一圈看作是60个单位长度,分针与时针相距30个单位长度,时针在前,分针在后,时针每分钟走$\frac{5}{60}$个单位长,分针每分钟走一个单位长,两针同向而行,何时分针追上时针;
(2)分针和时针在一条直线上有2种情况:时针分针成0°或180°角,根据这两种情况分别建立等量关系,列方程求解;
(3)时针在四点与五点之间,时针与分针有2种可能会成直角,四点与五点成30度角,时针每分钟走0.5度,而分针每分钟走6度.并且时针与分针成直角分两种情况:时针在分针前面时,时针在分针后面时,进行讨论.
解答 解:(1)设在6点过7分钟后,两针重合,
由题意得:x-$\frac{5}{60}$x=30,
解这个方程得:x=32$\frac{8}{11}$.
答:两针在6点32$\frac{8}{11}$分时重合.
(2)当时针分针成0°角时,即分针比时针多走35个单位长度;
x-$\frac{5}{60}$x=35
x=38$\frac{2}{11}$
即7点38$\frac{2}{11}$分时分针和时针成直线;
当时针分针成180°角时,即分针比时针多走35+30=65个单位长度;
x-$\frac{5}{60}$x=65
x=70$\frac{10}{11}$
即8点10$\frac{10}{11}$时分针和时针成直线;(不合题意,舍去)
答:7点38$\frac{2}{11}$分时分针和时针成直线.
解:时针每分钟走0.5度,而分针每分钟走6度,4点钟时针与分针角度为120度,设时针在四点x分钟时,时针与分针成直角,分两种情况讨论:
(3)时针在分针前面时,
120-6x+0.5x=90
解得x=5$\frac{5}{11}$
时针在分针后面时,
6x-120-0.5x=90
解得x=38$\frac{2}{11}$
所以在4时5$\frac{5}{11}$分或4时38$\frac{2}{11}$分,时针与分针成直角.
点评 此题考查一元一次方程的实际运用,把问题转化为行程问题中的追击问题是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
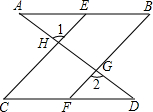 完成下面的证明过程:
完成下面的证明过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
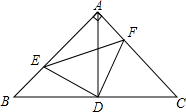 如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF
如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
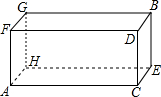 有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.
有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
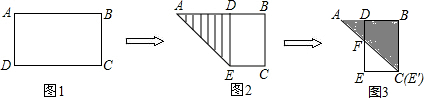
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com