
分析 (1)根据涨价时,每涨价1元,每星期要少卖出10件,可列出销售量的代数式,根据总利润=单件利润×销售量列出函数表达式即可;
(2)根据总利润=单件利润×销售量列出函数表达式即可;
(3)根据涨价的函数表达式,利用二次函数的性质解答.
解答 解:(1)∵每涨价1元,每星期要少卖出10件,
∴每星期实际可卖出(300-10x)件,
y=(60-40+x)(300-10x)=-10x2+100x+6000
∵$\left\{\begin{array}{l}{300-10x≥0}\\{x≥0}\end{array}\right.$,
∴0≤x≤30;
故答案为:(300-10x),-10x2+100x+6000,0≤x≤30;
(2)设每件降价m元,则毎星期售出商品的利润w,则
W=(20-m)(300+20m)=-20m2+100m+6000,
故答案为:-20m2+100m+6000;
(3)y=-10x2+100x+6000=-10(x-5)2+6250.
∴在涨价的情况下,每星期售出商品的最大利润是6250元.
点评 本题考查了二次函数的应用:根据实际问题列出二次函数关系式,再配成抛物线的顶点式y=a(x-h)2+k,然后利用当a<0,x=h时,y有最大值k;当a>0,x=h时,y有最小值k等性质解决实际问题


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
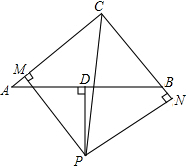 如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.
如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com