
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=8,tanA=$\frac{3}{4}$,求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=8,tanA=$\frac{3}{4}$,求CD的长.  教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:解答题
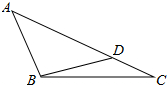 已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.
已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
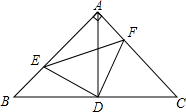 如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF
如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
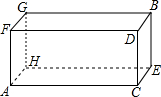 有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.
有一长方体纸盒,如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长AC为12.宽CE为9.高CD为7,请你帮助该小组计算出由A到B的最短路线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com