
 如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.
如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.  全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.9×102 | B. | 6.9×103 | C. | 6.9×107 | D. | 6.9×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
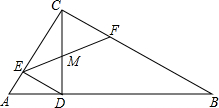 已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.
已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 函数图象经过点(0,0) | B. | 函数图象不经过第四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x为何值,总有y>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
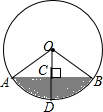 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com