
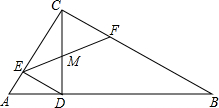
 已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.
已知△ABC中,∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.分析 (1)由已知条件易求BC、AB的长,再根据△ACB的面积为定值即可求出CD的长,
(2)若△EFC与△ABC相似,则CE可以和BC为对应边,也可以和AC为对应边,所以此题要分两种情况讨论求出CF的长,再由△DEM∽△CFM即可求出不同情况下EM的长.
解答 解:(1)∵∠ACB=90°,AC=3,tanA=$\frac{4}{3}$,
∴BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵CD⊥AB于点D,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴CD=2.4;
(2)∵CD⊥AB于点D,tanA=$\frac{4}{3}$,AC=3,
∴AD=$\frac{9}{5}$,
∵DE⊥AC,tanA=$\frac{4}{3}$,
∴AE=$\frac{27}{20}$,DE=$\frac{36}{27}$,
∴CE=3-$\frac{27}{20}$=$\frac{33}{20}$,
若△EFC与△ABC相似,
则$\frac{CE}{AC}=\frac{CF}{BC}=\frac{EF}{AB}$或$\frac{CE}{BC}=\frac{CF}{AC}=\frac{EF}{AB}$,
解得:CF=$\frac{11}{5}$或$\frac{99}{80}$,EF=$\frac{11}{4}$或$\frac{33}{16}$,
∵DE⊥AC,BC⊥AC,
∴△DEM∽△CFM,
∴$\frac{DE}{CF}=\frac{EM}{FM}$,
∴EM=$\frac{144}{125}$或$\frac{6}{5}$.
点评 本题考查了相似三角形的判定和性质、锐角三角函数的运用、勾股定理的运用以及三角形面积公式的运用,题目对学生的计算能力要求很高,注意分类讨论的数学思想运用是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.
如图,是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,它与x轴的一个交点为A(3,0),根据图象,可知关于x的一元二次方程ax2+bx+c=0的解是3或-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com