
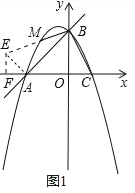
����Ŀ����ͼ����ֱ֪��y��x+2��x�ᡢy��ֱ��ڵ�A��B��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����![]() ���������߾���A��B���㣬��x������һ��C��
���������߾���A��B���㣬��x������һ��C��
��1���������ߵĽ���ʽ��
��2����M��������x���Ϸ�һ�㣬��MBA����CBO�����M�����ꣻ
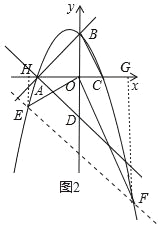
��3������A��AB�Ĵ��߽�y���ڵ�D��ƽ��ֱ��AD���������ڵ�E��F���㣬����EO��FO������EFOΪ��EFΪб�ߵ�ֱ�������Σ���ƽ�ƺ��ֱ�ߵĽ���ʽ��

���𰸡���1��y����x2��x+2����2��M����![]() ��
��![]() ������3��ƽ�ƺ�Ľ���ʽΪy����x��1+
������3��ƽ�ƺ�Ľ���ʽΪy����x��1+![]() ��y����x��1��
��y����x��1��![]() ��
��
��������
��1�����ô���ϵ�������ɽ�����⣻
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F�������E���꣬�����ֱ��BE�Ľ���ʽ�����÷����鼴�ɽ�����⣻
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G���������������ε������Լ�����ϵ����ϵ���������鼴�ɽ�����⣻
��1����ֱ��y��x+2��x�ᡢy��ֱ��ڵ�A��B��
��A����2��0����B��0��2����
�������ߵĶԳ���x����![]() ��A��C���ڶԳ���Գƣ�
��A��C���ڶԳ���Գƣ�
��C��1��0����
�������ߵĽ���ʽΪy��a��x+2����x��1�����ѣ�0��2������õ�a����1��
�������ߵĽ���ʽΪy����x2��x+2��
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F��
�ߡ�ABE����OBC����BAE����BOC��90�㣬
���BAE�ס�BOC��
��![]() ��
��
��![]() ��
��
��AE��![]() ��
��
�ߡ�EAF+��BAO��90�㣬��BAO��45�㣬
���EAF��45�㣬
��EF��AF��1��
��E��3��1����
��ֱ��BE�Ľ���ʽΪy����![]() x+2��
x+2��
��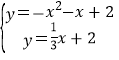 �����
�����![]() ��
��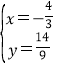 ��
��
��M��-![]() ��
��![]() ����
����
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G��
�ߡ�EOF=90��=��PHE=��OGF��
����EHO�ס�OGF�õ���
![]() ��
��
��![]() ��
��
��x1x2+y1y2=0��
��![]() ����ȥy�õ���x2+b-2=0��
����ȥy�õ���x2+b-2=0��
��x1x2=b-2��x1+x2=0��y1y2=��-x1+b����-x2+b��=x1x2+b2��
��2��b-2��+b2=0��
���b=-1-![]() ��-1+
��-1+![]() ����������
����������
��ֱ��AD����ƽ��ʱ��ͬ���ɵ�b=-1+![]() ��
��
����������ƽ�ƺ�Ľ���ʽΪy=-x-1+![]() ��y=-x-1-
��y=-x-1-![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A�ŷ���װ�����ſ�Ƭ����Ƭ�Ϸֱ�д��4cm��2cm��B�ŷ���װ�����ſ�Ƭ����Ƭ�Ϸֱ�д��3cm��5cm��2cm��A��B�ŷ�����һ��д��5cm�Ŀ�Ƭ�����п�Ƭ����״����С��ȫ��ͬ��������������ŷ��и�ȡһ�ſ�Ƭ�����ŷ���Ŀ�Ƭ����һ���ÿ�Ƭ�ϱ��������ֱ���Ϊ�����߶εij��ȣ�
��1�����������߶�����������εĸ��ʣ��оٷ����б���������ͼ������
��2�����������߶������ֱ�������εĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��8x��k2��0��kΪ��������
��1����֤����������������ȵ�ʵ������
��2����x1��x2Ϊ���̵�����ʵ��������x1+2x2��7����������̵�����ʵ������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪��C��90�㣬sin��A��![]() ����DΪ��AC��һ�㣬����BDC��45�㣬DC��6cm,���ABC��������� ________cm2.
����DΪ��AC��һ�㣬����BDC��45�㣬DC��6cm,���ABC��������� ________cm2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����A����1��0������B��3��0������C��4��y1��������D��x2��y2����������������һ�㣬�����н��ۣ�
�ٶ��κ���y=ax2+bx+c����СֵΪ��4a��
������1��x2��4����0��y2��5a��
����y2��y1����x2��4��
��һԪ���η���cx2+bx+a=0��������Ϊ��1��![]()
������ȷ���۵ĸ����ǣ�������
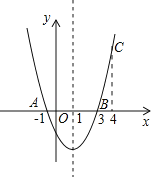
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��ACƽ�֡�BAD,�ӳ�DC��AB���ӳ����ڵ�E ��
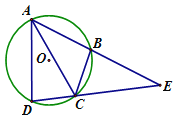
��1������ADC=86�㣬���CBE�Ķ�����
��2����AC=EC����֤��AD=BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һЩ�ⳤΪ1��С��������������������ͼ�������������Ļ����ϣ����ı�ԭ��������С�������λ�ã�������������ͬ��С�����飬�Դ��һ�������壬���ٻ���Ҫ________��С�����飮���մ�ɵij�����ı������________��
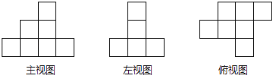
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣���ͼ��ʾ��ij��ѧ�С��ѡ������С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30������������������6�����µ�A������A����ô�������B��������48��. ���½���FAE=30����������ĸ߶�. ����������������ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijһ���������Ա���x�ڹ涨�ķ�Χ�ڣ�������ȡ����ֵx1��x2�����ǵĶ�Ӧ����ֵ�ֱ�Ϊy1��y2�� ��x2��x1ʱ����y2��y1����Ƹú���������������x2��x1ʱ����y2��y1����Ƹú��������ݼ���������κ���y=x2����x��0ʱ���ú���������������x��0ʱ���ú��������ݼ���
��1�����κ�����y=��x+1��2+2�Ա���x���ĸ���Χ�ڣ��ú��������ݼ���
��2��֤����������y=x��![]() ��x��1�ĺ�����Χ�ڣ��ú�������������
��x��1�ĺ�����Χ�ڣ��ú�������������
��3����������������x��һ�κ������ֱ��Ϊ��g=k1x+b1��h=k2x+b2���Һ���g��ʵ����Χ�ڵ�������������h��ʵ����Χ�ڵ����ݼ����ǵ�����һ�κ���y=g+h�������ϵ��k1��k2�����������ʱ������y��ʵ����Χ�ڵ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com