
����Ŀ������ijһ���������Ա���x�ڹ涨�ķ�Χ�ڣ�������ȡ����ֵx1��x2�����ǵĶ�Ӧ����ֵ�ֱ�Ϊy1��y2�� ��x2��x1ʱ����y2��y1����Ƹú���������������x2��x1ʱ����y2��y1����Ƹú��������ݼ���������κ���y=x2����x��0ʱ���ú���������������x��0ʱ���ú��������ݼ���
��1�����κ�����y=��x+1��2+2�Ա���x���ĸ���Χ�ڣ��ú��������ݼ���
��2��֤����������y=x��![]() ��x��1�ĺ�����Χ�ڣ��ú�������������
��x��1�ĺ�����Χ�ڣ��ú�������������
��3����������������x��һ�κ������ֱ��Ϊ��g=k1x+b1��h=k2x+b2���Һ���g��ʵ����Χ�ڵ�������������h��ʵ����Χ�ڵ����ݼ����ǵ�����һ�κ���y=g+h�������ϵ��k1��k2�����������ʱ������y��ʵ����Χ�ڵ���������
���𰸡���1��x��-1ʱ�������ݼ���2��֤����������3��һ�κ���y=g+h�������ϵ��k1��k2����k1��0��k2��0��k1+k2��0ʱ������y��ʵ����Χ�ڵ�������
��������
��1������a��0�����κ������Ա����ڶԳ��������ݼ����ɵô𰸣�
��2������y��x����������ɵ�֤���Ľ��ۣ�
��3������һ�κ��������ʣ��ɵô𰸣�
��1��y=��x+1��2+2�Ա�����x�ܩ�1��Χ�ڣ��ú��������ݼ���
��2��֤������ȡ x2��x1 ��
��![]() =��x2��x1��+��
=��x2��x1��+��![]() ��
��
=��x2��x1��+��![]() ��
��
��Ϊx2��x1 �� ����y2��y1
��y=x��![]() ��x��1�ĺ�����Χ�ڣ��ú�������������
��x��1�ĺ�����Χ�ڣ��ú�������������
��3����g=k1x+b1��h=k2x+b2 �� �Һ���g��ʵ����Χ�ڵ�������������h��ʵ����Χ�ڵ����ݼ���
��k1��0��k2��0��
y=g+h
��y=��k1x+b1��+��k2x+b2��=��k1+k2��x+��b1+b2��
y=��k1+k2��x+��b1+b2������������
��k1+k2��0��
һ�κ���y=g+h�������ϵ��k1��k2����k1��0��k2��0��k1+k2��0ʱ������y��ʵ����Χ�ڵ���������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��x+2��x�ᡢy��ֱ��ڵ�A��B��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����![]() ���������߾���A��B���㣬��x������һ��C��
���������߾���A��B���㣬��x������һ��C��
��1���������ߵĽ���ʽ��
��2����M��������x���Ϸ�һ�㣬��MBA����CBO�����M�����ꣻ
��3������A��AB�Ĵ��߽�y���ڵ�D��ƽ��ֱ��AD���������ڵ�E��F���㣬����EO��FO������EFOΪ��EFΪб�ߵ�ֱ�������Σ���ƽ�ƺ��ֱ�ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
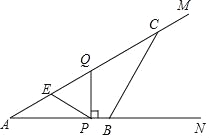
����Ŀ����ͼ����MAN��30�㣬��C��B�ֱ�������AM��AN�ϣ�AB��6����ACB��30�㣮����P�ӵ�A������������AN��ÿ��3����λ���ȵ��ٶ��˶�������P��PQ��AN������AM�ڵ�Q����E���߶�AQ���е㣬����PE�����PQE���ABC�ص�����ͼ�ε����ΪSƽ����λ����P���˶�ʱ��Ϊt�루t��O����
��1����PQ�ij����ú�t�Ĵ���ʽ��ʾ����
��2������Q�ڱ�AC��ʱ����S��t֮��ĺ�����ϵʽ��
��3������PQE���ABC�ص�����ͼ����һ�����Ϊ![]() ��������ʱ����t��ֵ��
��������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ı�AB��x���ϣ���C������Ϊ����5��4������D��y����������ϣ�������A��ֱ��y��![]() x��1��y�ύ�ڵ�E����ֱ��AE��y������ƽ��n��n��0������λ���Ⱥõ�ֱ��l��ֱ��l������Cʱֹͣƽ�ƣ�
x��1��y�ύ�ڵ�E����ֱ��AE��y������ƽ��n��n��0������λ���Ⱥõ�ֱ��l��ֱ��l������Cʱֹͣƽ�ƣ�

��1����A�������� ������B�������� ����
��2����ֱ��l��y���ڵ�F������CF�����CDF�����ΪS������涨���߶������Ϊ0�������Σ�����S��n֮��ĺ�����ϵʽ����д��n��ȡֵ��Χ��
��3����֪AE��AD�ڵ�A,��ֱ��l������AD��DC�ڵ�P������AEPΪֱ��������ʱ����ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
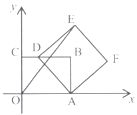
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����OABC�Ķ���A��x���ϣ�OA=4��OC=3����DΪBC����һ�㣬��ADΪһ�������B��ͬ����������ADEF������OE������D�ڱ�BC���˶�ʱ��OE�ij��ȵ���Сֵ��________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ������(�����B��C��D�غ�)�����ı���OBCD��ƽ���ı���ʱ����ô![]() ��������ϵ��________________.
��������ϵ��________________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��ʼ������
��ʼ������![]() ��
��![]() ���ٶ��˶�����
���ٶ��˶�����![]() ��
��![]() ��ʼ��
��ʼ��![]() ����
����![]() ���ٶ��ƶ��������
���ٶ��ƶ��������![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ������������һ�㵽��
ͬʱ������������һ�㵽��![]() ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() ����
����![]() ________ʱ���ı���
________ʱ���ı���![]() ҲΪ���Σ�
ҲΪ���Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����֪BC����O��ֱ����AC����O�ڵ�C��AB����O�ڵ�D��EΪAC���е㣬����DE��
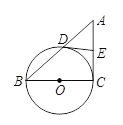
��1����AD=DB��OC=5��������AC�ij���
��2����֤��ED����O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣮
��1������������B��Բ��O��б��AB�������AC�����ڵ�E�ġ�O��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д������֤����
��2���裨1���������ġ�O���AB�������ڵ�B������һ��D������O��ֱ��Ϊ5��BC��4����DE�ij���������ó߹���ͼ������ͼ�Σ��ɻ�����ͼ��ɣ�2���ʣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com