
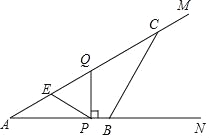
【题目】如图,∠MAN=30°,点C、B分别在射线AM、AN上,AB=6,∠ACB=30°.动点P从点A出发,沿射线AN以每秒3个单位长度的速度运动.过点P作PQ⊥AN交射线AM于点Q,点E是线段AQ的中点,连结PE.设△PQE与△ABC重叠部分图形的面积为S平方单位,点P的运动时间为t秒(t>O).
(1)求PQ的长(用含t的代数式表示).
(2)当点Q在边AC上时,求S与t之间的函数关系式.
(3)当△PQE与△ABC重叠部分图形是一个面积为![]() 的三角形时,求t的值.
的三角形时,求t的值.
【答案】(1)![]() (2)
(2)![]() (3)t=1或t=6﹣
(3)t=1或t=6﹣![]()
【解析】
(1)在直角三角形根据正切公式直接求.
(2)分类讨论当t不同时,两者的关系,再综合描述即可.
(3) 分类讨论当t不同时,形成固定面积三角形时的t值即可.
解:(1)在Rt△APQ中,∠MAN=30°,AP=3t,
∴PQ=APtan∠MAN=![]() t;
t;
(2)当0<t≤2时,如图,
∵点E是线段AQ的中点,
S=![]() S△APQ=
S△APQ=![]() ×AP×PQ=
×AP×PQ=![]() ×3t×
×3t×![]() t=
t=![]() t2,
t2,
当2<t≤3时,如图2,
∵∠MAN=30°,∠ACB=30°,
∴∠CBP=60°,
∵PQ⊥AN,点E是线段AQ的中点,
∴EA=EP,
∴∠EPA=∠A=30°,
∴∠BGP=90°,
由题意得,BP=3t﹣6,
∴PG=![]() (3t﹣6),
(3t﹣6),
∴GH=![]() ×
×![]() (3t﹣6)=
(3t﹣6)=![]() (3t﹣6),
(3t﹣6),
∴S△PGH=![]() ×GP×GH=
×GP×GH=![]() (3t﹣6)2,
(3t﹣6)2,
∴S=![]() t2﹣
t2﹣![]() (3t﹣6)2=﹣
(3t﹣6)2=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ;
;
(3)当0<t≤2时,![]() t2=
t2=![]() ,
,
解得,t1=1,t2=﹣1(不合题意,舍去),
当2<t≤3时,△PQE与△ABC重叠部分图形是四边形.
当3<t≤6时,S=![]() (6
(6![]() ﹣
﹣![]() t)2=
t)2=![]() (6﹣t)2,
(6﹣t)2,
则![]() (6﹣t)2=
(6﹣t)2=![]() ,
,
解得,t1=6﹣![]() ,t2=6+
,t2=6+![]() (不合题意,舍去).
(不合题意,舍去).
综上,t=1或t=6﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣8x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=7,试求出方程的两个实数根和k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
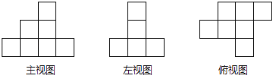
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在抛物线y=x2﹣2x+2上运动,过点A作AC上x轴于点C,以AC为对角线作矩形ABCD,连结BD,则BD的最小值为( )
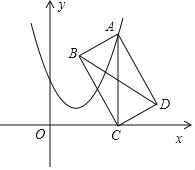
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
(1)中国古代数学著作《周髀算经》有着这样的记载:“勾广三,股修四,经隅五.”这句话的意思是:“如果直角三角形两直角边为3和4时,那么斜边的长为5.”上述记载说明:在![]() 中,如果
中,如果![]() ,
,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 三者之间的数量关系是: .
三者之间的数量关系是: .
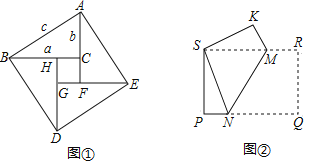
(2)对于(1)中这个数量关系,我们给出下面的证明.如图①,它是由四个全等的直角三角形围成的一个大正方形![]() ,中空的部分是一个小正方形
,中空的部分是一个小正方形![]() .结合图①,将下面的证明过程补充完整:
.结合图①,将下面的证明过程补充完整:
∵![]() ,
,![]()
![]() (用含
(用含![]() 的式子表示)
的式子表示)
又∵ ![]() .
.
∴![]()
∴![]()
∴ .
(3)如图②,把矩形![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 处,折痕为
处,折痕为![]() .如果
.如果![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一个函数,自变量x在规定的范围内,若任意取两个值x1和x2,它们的对应函数值分别为y1和y2. 若x2>x1时,有y2>y1,则称该函数单调递增;若x2>x1时,有y2<y1,则称该函数单调递减.例如二次函数y=x2,在x≥0时,该函数单调递增;在x≤0时,该函数单调递减.
(1)二次函数:y=(x+1)2+2自变量x在哪个范围内,该函数单调递减?
(2)证明:函数:y=x﹣![]() 在x>1的函数范围内,该函数单调递增.
在x>1的函数范围内,该函数单调递增.
(3)若存在两个关于x的一次函数,分别记为:g=k1x+b1和h=k2x+b2,且函数g在实数范围内单调递增,函数h在实数范围内单调递减.记第三个一次函数y=g+h,则比例系数k1和k2满足何种条件时,函数y在实数范围内单调递增?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com