
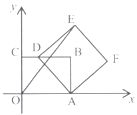
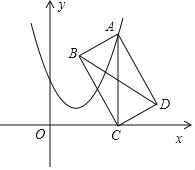
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE。当点D在边BC上运动时,OE的长度的最小值是________
【答案】5![]()
【解析】
过点D作DG⊥OA,过点E作HE⊥DG.先证明△HED≌△GDA,从而得到HE=DG=3,HD=AG.设D(a,3),则DC=a,DH=AG=4-a,则E(a+3,7-a),依据两点间的距离公式可得到OE=![]() ,最后利用配方法求得被开方数的最小值即可.
,最后利用配方法求得被开方数的最小值即可.
如图所示:过点D作DG⊥OA,过点E作HE⊥DG.
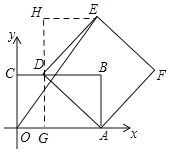
∵DG⊥OA,HE⊥DG,
∴∠EHD=∠DGA=90°.
∴∠GDA+∠DAG=90°.
∵四边形ADEF为正方形,
∴DE=AD,∠HDE+∠GDA=90°.
∴∠HDE=∠GAD.
在△HED和△GDA中
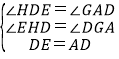 ,
,
∴△HED≌△GDA.
∴HE=DG=3,HD=AG.
设D(a,3),则DC=a,DH=AG=4-a.
∴E(a+3,7-a).
∴OE=![]() =
=![]() .
.
当a=2时,OE有最小值,最小值为5![]() .
.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
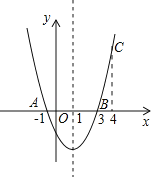
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在抛物线y=x2﹣2x+2上运动,过点A作AC上x轴于点C,以AC为对角线作矩形ABCD,连结BD,则BD的最小值为( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
(1)中国古代数学著作《周髀算经》有着这样的记载:“勾广三,股修四,经隅五.”这句话的意思是:“如果直角三角形两直角边为3和4时,那么斜边的长为5.”上述记载说明:在![]() 中,如果
中,如果![]() ,
,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 三者之间的数量关系是: .
三者之间的数量关系是: .
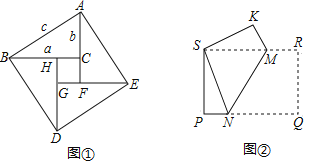
(2)对于(1)中这个数量关系,我们给出下面的证明.如图①,它是由四个全等的直角三角形围成的一个大正方形![]() ,中空的部分是一个小正方形
,中空的部分是一个小正方形![]() .结合图①,将下面的证明过程补充完整:
.结合图①,将下面的证明过程补充完整:
∵![]() ,
,![]()
![]() (用含
(用含![]() 的式子表示)
的式子表示)
又∵ ![]() .
.
∴![]()
∴![]()
∴ .
(3)如图②,把矩形![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 处,折痕为
处,折痕为![]() .如果
.如果![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
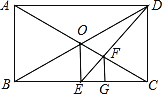
【题目】如图所示,在矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G.
(1)说明点G是线段BC的一个三等分点;
(2)请你依照上面的画法,在原图上画出BC的一个四等分点(保留作图痕迹,不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一个函数,自变量x在规定的范围内,若任意取两个值x1和x2,它们的对应函数值分别为y1和y2. 若x2>x1时,有y2>y1,则称该函数单调递增;若x2>x1时,有y2<y1,则称该函数单调递减.例如二次函数y=x2,在x≥0时,该函数单调递增;在x≤0时,该函数单调递减.
(1)二次函数:y=(x+1)2+2自变量x在哪个范围内,该函数单调递减?
(2)证明:函数:y=x﹣![]() 在x>1的函数范围内,该函数单调递增.
在x>1的函数范围内,该函数单调递增.
(3)若存在两个关于x的一次函数,分别记为:g=k1x+b1和h=k2x+b2,且函数g在实数范围内单调递增,函数h在实数范围内单调递减.记第三个一次函数y=g+h,则比例系数k1和k2满足何种条件时,函数y在实数范围内单调递增?
查看答案和解析>>
科目:初中数学 来源: 题型:
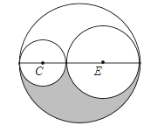
【题目】如图所示,两个小圆的半径分别是2厘米和3厘米,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
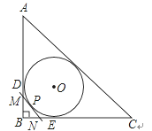
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com