
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
 解:(1)由y=
解:(1)由y=| 1 |
| 2 |
| 12+22 |
| 5 |
| 5 |
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
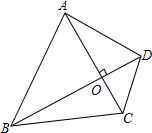 如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.
如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
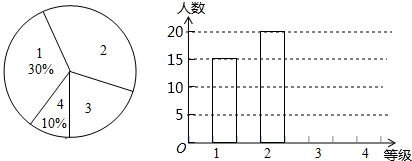 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
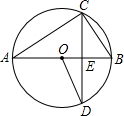 如图,AB是⊙O的直径,CD是弦,AB⊥CD垂足为点 E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD垂足为点 E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为( )A、
| ||
B、2
| ||
C、3
| ||
D、4
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、13,13 |
| B、14,14 |
| C、13,14 |
| D、14,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
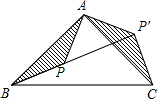 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,使△ABP绕点A旋转后,与△ACP′重合.若AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,使△ABP绕点A旋转后,与△ACP′重合.若AP=| 2 |
| A、2 | ||
B、
| ||
C、
| ||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| A、7 | B、6.5 | C、6 | D、9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com