
【题目】△ABC内接于⊙O,AC为⊙O的直径,∠A=60°,点D在AC上,连接BD作等边三角形BDE,连接OE.
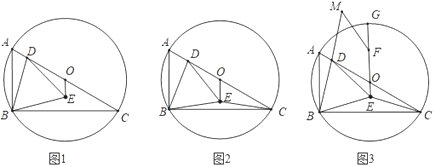
(1)如图1,求证:OE=AD;
(2)如图2,连接CE,求证:∠OCE=∠ABD;
(3)如图3,在(2)的条件下,延长EO交⊙O于点G,在OG上取点F,使OF=2OE,延长BD到点M使BD=DM,连接MF,若tan∠BMF=![]() ,OD=3,求线段CE的长.
,OD=3,求线段CE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)CE=![]() .
.
【解析】
(1)连接OB,证明△ABD≌△OBE,即可证出OE=AD.
(2)连接OB,证明△OCE≌△OBE,则∠OCE=∠OBE,由(1)的全等可知∠ABD=∠OBE,则∠OCE=∠ABD.
(3)过点M作AB的平行线交AC于点Q,过点D作DN垂直EG于点N,则△ADB≌△MQD,四边形MQOG为平行四边形,∠DMF=∠EDN,再结合特殊角度和已知的线段长度求出CE的长度即可.
解:(1)如图1所示,连接OB,
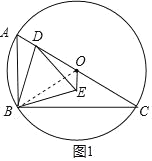
∵∠A=60°,OA=OB,
∴△AOB为等边三角形,
∴OA=OB=AB,∠A=∠ABO=∠AOB=60°,
∵△DBE为等边三角形,
∴DB=DE=BE,∠DBE=∠BDE=∠DEB=60°,
∴∠ABD=∠OBE,
∴△ADB≌△OBE(SAS),
∴OE=AD;
(2)如图2所示,
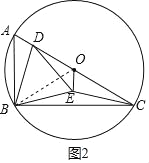
由(1)可知△ADB≌△OBE,
∴∠BOE=∠A=60°,∠ABD=∠OBE,
∵∠BOA=60°,
∴∠EOC=∠BOE =60°,
又∵OB=OC,OE=OE,
∴△BOE≌△COE(SAS),
∴∠OCE=∠OBE,
∴∠OCE=∠ABD;
(3)如图3所示,过点M作AB的平行线交AC于点Q,过点D作DN垂直EG于点N,
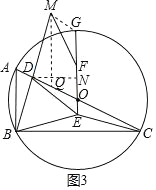
∵BD=DM,∠ADB=∠QDM,∠QMD=∠ABD,
∴△ADB≌△MQD(ASA),
∴AB=MQ,
∵∠A=60°,∠ABC=90°,
∴∠ACB=30°,
∴AB=![]() =AO=CO=OG,
=AO=CO=OG,
∴MQ=OG,
∵AB∥GO,
∴MQ∥GO,
∴四边形MQOG为平行四边形,
设AD为x,则OE=x,OF=2x,
∵OD=3,
∴OA=OG=3+x,GF=3﹣x,
∵DQ=AD=x,
∴OQ=MG=3﹣x,
∴MG=GF,
∵∠DOG=60°,
∴∠MGF=120°,
∴∠GMF=∠GFM=30°,
∵∠QMD=∠ABD=∠ODE,∠ODN=30°,
∴∠DMF=∠EDN,
∵OD=3,
∴ON=![]() ,DN=
,DN=![]() ,
,
∵tan∠BMF=![]() ,
,
∴tan∠NDE=![]() ,
,
∴ ,
,
解得x=1,
∴NE=![]() ,
,
∴DE=![]() ,
,
∴CE=![]() .
.
故答案为(1)证明见解析;(2)证明见解析;(3)CE=![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在半圆![]() 中,直径
中,直径![]() 的长为6,点
的长为6,点![]() 是半圆上一点,过圆心
是半圆上一点,过圆心![]() 作
作![]() 的垂线交线段
的垂线交线段![]() 的延长线于点
的延长线于点![]() ,交弦
,交弦![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)记![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形:

(1)可知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值,具体解法如下:
,用“画图法”求tan(α+β)的值,具体解法如下:
第一步:如图1所示,构造符合题意两个“背靠背”的直角三角形;
第二步:如图2所示,将图1中所有数据同比例扩大3倍;
第三步:如图3所示,依托中间的Rt△ABD的各顶点构造“水平﹣﹣竖直辅助线”,构造出“一线三直角”基本相似型,并补成矩形ACEF;由图可知tan(α+β)= .
(2)依据(1)的方法,已知tanα=![]() ,tanβ=
,tanβ=![]() ,用“画图法”求tan(α+β)的值.
,用“画图法”求tan(α+β)的值.
(3)扩展延伸,已知tanα=![]() ,tanβ=
,tanβ=![]() ,直接写出tan(α﹣β)= .
,直接写出tan(α﹣β)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,将矩形ABCD折叠,使点C与点A重合,点D落在点G处,折痕为EF.
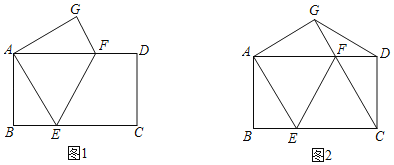
(1)如图1,求证:BE=GF;
(2)如图2,连接CF、DG,若CE=2BE,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形都为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
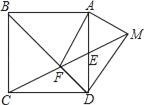
【题目】如图,边长为4正方形ABCD中,E为边AD的中点,连接线段EC交BD于点F,点M是线段CE延长线上的一点,且∠MAF为直角,则DM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备从文教商店购买A、B两种不同型号的笔记本奖励学生,已知购买2本A型和3本B型笔记本共需23元,购买3本A型和4本B型笔记本共需32元
(1)分别求出A、B型笔记本的单价?
(2)学校准备购买A、B两种笔记本共100本,经过协商文教店老板给一定的优惠,A型笔记本打九折,B型笔记本打八折,已知A型笔记本进价2.6元,B型笔记本进价2.8元,若文教店老板想这次交易中赚到不少于110元钱,则卖出A型笔记本不超过多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校举行校园歌唱大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列题:
(1)请将条形统计图补全;
(2)获得一等奖的同学中有![]() 来自七年级,有
来自七年级,有![]() 来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加全市校园歌唱大赛,请通过列表或画树状图求所选出的两人中有七年级或八年级同学的概率.
来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加全市校园歌唱大赛,请通过列表或画树状图求所选出的两人中有七年级或八年级同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 的延长线上,延长
的延长线上,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求
,求![]() 的值及
的值及![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com