【题目】学校准备从文教商店购买A、B两种不同型号的笔记本奖励学生，已知购买2本A型和3本B型笔记本共需23元，购买3本A型和4本B型笔记本共需32元
（1）分别求出A、B型笔记本的单价？
（2）学校准备购买A、B两种笔记本共100本，经过协商文教店老板给一定的优惠，A型笔记本打九折，B型笔记本打八折，已知A型笔记本进价2.6元，B型笔记本进价2.8元，若文教店老板想这次交易中赚到不少于110元钱，则卖出A型笔记本不超过多少本？
【答案】（1）购买一本A型笔记本和一本B型笔记本分别需要4元、5元；（2）卖出A型笔记本不超过50本．
【解析】
（1）设购买一本A型笔记本和一本B型笔记本分别需要x元、y元，根据单价乘以数量等于总价建立方程组求解即可；
（2）设卖出A型笔记本不超过a本，则B型笔记本为(100﹣a)本，根据打折情况分别表示两种笔记本的利润，再根据总利润不少于110元建立不等式求解．
解：（1）设购买一本A型笔记本和一本B型笔记本分别需要x元、y元，
根据题意得，
，解得：
，
答：购买一本A型笔记本和一本B型笔记本分别需要4元、5元；
（2）设卖出A型笔记本不超过a本，则B型笔记本为(100﹣a)本，
根据题意得，
解得：a≤50，
答：卖出A型笔记本不超过50本．
科目：初中数学 来源： 题型：
【题目】一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：
会员年卡类型 | 办卡费用（元） | 每次游泳收费（元） |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如，购买A类会员年卡，一年内游泳20次，消费50+25×20＝550元，若一年内在该游泳馆游泳的次数介于40～50次之间，则最省钱的方式为（ ）
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC内接于⊙O，AC为⊙O的直径，∠A＝60°，点D在AC上，连接BD作等边三角形BDE，连接OE．
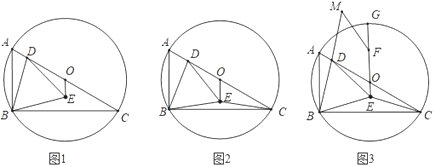
(1)如图1，求证：OE＝AD；
(2)如图2，连接CE，求证：∠OCE＝∠ABD；
(3)如图3，在(2)的条件下，延长EO交⊙O于点G，在OG上取点F，使OF＝2OE，延长BD到点M使BD＝DM，连接MF，若tan∠BMF＝
，OD＝3，求线段CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2017山东省菏泽市，第20题，7分）如图，一次函数y=kx+b与反比例函数
的图象在第一象限交于A、B两点，B点的坐标为（3，2），连接OA、OB，过B作BD⊥y轴，垂足为D，交OA于C，若OC=CA．
（1）求一次函数和反比例函数的表达式；
（2）求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
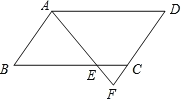
【题目】如图，在平行四边形ABCD中，点E在边BC上，射线AE交DC的延长线于点F，已知BE=3CE，△ABE的周长为9，则△ADF的周长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
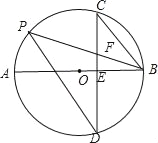
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，弦PB与CD交于点F，且FC＝FB．
（1）求证：PD∥CB；
（2）若AB＝26，EB＝8，求CD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】规定：[x]表示不大于x 的最整数，(x) 表示不小于x的最小整数，[x) 表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，(2.3)=3，[2.3)=2，则下列说法正确的是__________（写出所有正确说法）.
①当x=1.7时，[x]+(x)+[x)=6；
②当x=-2.1时，[x]+(x)+[x)=-7；
③方程4[x]+3(x)+[x)=11的解为1<x<1.5；
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析：（1）根据题目中给的计算方法代入计算后判定即可；（2）根据题目中给的计算方法代入计算后判定即可；（3）根据题目中给的计算方法代入计算后判定即可；（4）结合x的取值范围，分类讨论，利用题目中给出的方法计算后判定即可.
详解：
①当x=1.7时，
[x]+（x）+[x）
=[1.7]+（1.7）+[1.7）=1+2+2=5，故①错误；
②当x=﹣2.1时，
[x]+（x）+[x）
=[﹣2.1]+（﹣2.1）+[﹣2.1）
=（﹣3）+（﹣2）+（﹣2）=﹣7，故②正确；
③当1＜x＜1.5时，
4[x]+3（x）+[x）
=4×1+3×2+1
=4+6+1
=11，故③正确；
④∵﹣1＜x＜1时，
∴当﹣1＜x＜﹣0.5时，y=[x]+（x）+x=﹣1+0+x=x﹣1，
当﹣0.5＜x＜0时，y=[x]+（x）+x=﹣1+0+x=x﹣1，
当x=0时，y=[x]+（x）+x=0+0+0=0，
当0＜x＜0.5时，y=[x]+（x）+x=0+1+x=x+1，
当0.5＜x＜1时，y=[x]+（x）+x=0+1+x=x+1，
∵y=4x，则x﹣1=4x时，得x=
；x+1=4x时，得x=
；当x=0时，y=4x=0，
∴当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有三个交点，故④错误，
故答案为：②③．
点睛：本题是阅读理解题，前三问比较容易判定，根据题目所给的方法判定即可；第四问较难，结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值： 
，其中
， 
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
