
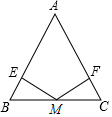
 如图,△ABC中,AB=AC,M是BC的中点,过点M作ME⊥AB、MF⊥AC,垂足分别为E、F.求证:ME=MF.
如图,△ABC中,AB=AC,M是BC的中点,过点M作ME⊥AB、MF⊥AC,垂足分别为E、F.求证:ME=MF.  阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
| 用水量 | 单价 |
| 0<x≤22 | a |
| 剩余部分 | a+1.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{5}$=2$\sqrt{5}$ | B. | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C. | (-2a2)3=-6a6 | D. | (x+1)2=x2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a-1}-\frac{1}{a-1}=1$ | B. | $\frac{m}{{{m^2}+1}}=\frac{1}{m+1}$ | C. | $\frac{{{x^2}-1}}{x-1}=x-1$ | D. | $\frac{-a-1}{a+1}=-\frac{a-1}{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
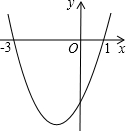 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.
李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com