
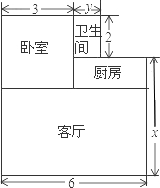
 老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.
老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.分析 (1)①根据长方形的面积=长×宽,求出卫生间面积是多少即可;②根据长方形的面积=长×宽,用长是y+3、宽是2的长方形的面积加上长是6、宽是x的长方形的面积,即可求出地面总面积是多少.
(2)首先根据地面总面积是卫生间面积的10倍,可得客厅、卧室、厨房的总面积是卫生间面积的9倍,然后根据客厅、卧室、厨房的总面积比卫生间面积多32m2,求出卫生间的面积是多少,再用卫生间的面积乘以10,求出地面总面积是多少;最后根据总价=单价×面积,用铺1m2地砖的平均费用乘以地砖的面积,求出铺地砖的总费用为多少元即可.
解答 解:(1)如图,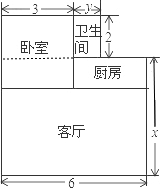 ,
,
①卫生间面积:2y;
②地面总面积:
2(y+3)+6x=6x+2y+6.
(2)因为地面总面积是卫生间面积的10倍,
所以客厅、卧室、厨房的总面积是卫生间面积的9倍,
80×[32÷(9-1)×10]
=80×[4×10]
=80×40
=3200(元)
答:铺地砖的总费用为3200元.
故答案为:2y、6x+2y+6.
点评 (1)此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)此题还考查了长方形的面积的求法,要熟练掌握,解答此题的关键是要明确:长方形的面积=长×宽.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
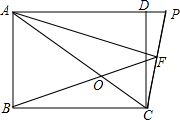 已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.
已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
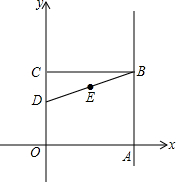 如图,O是坐标原点,矩形OABC的顶点A在z轴的正半轴上,点C在y轴的正半轴上,点D在边OC上,且点B(6,5),tan∠CBD=$\frac{1}{3}$.
如图,O是坐标原点,矩形OABC的顶点A在z轴的正半轴上,点C在y轴的正半轴上,点D在边OC上,且点B(6,5),tan∠CBD=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
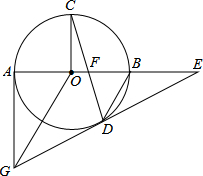 如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.
如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com